A man of height h0=2m is bungee jumping from a platform situated at a height h = 25 m above a lake One end of an elastic rope is attached to his foot and the other end is fixed to the platform He starts falling from rest in vertical position. The length and elastic properties of the rope are chosen so that his speed will have been reduced to zero at instant when his head reaches the surface of water. Ultimetely the jumper is hanging from the rope with his head 8m above the water. Find the maxima acceleration acheived during the jump in m/s2)

The correct Answer is:40
Let us denote the elastic constant (spring constant) of the rope by k and its unstretched length by l0 The maximum length of the rope is l1=h−h0=23 m whilst in equilibrium it is l2=(23−8)m=15m initially and at the jumper's lowest position, the kinetic energy is zero if we ignore the mass of the rope and assume that the jumper's centre of mass is half - way up his body, we can use conservation of energy to write mgh=12k(l1−l0)2
In addition in equilibrium mg=k(l2−l0)
Dividing the two equations by each other we obtain a quadratic equation for l_(0)
l20+2(h−l1)l0+(l21−2hl2)=l20+4l0−221=0
which gives l0=13m
When the falling jumper attains his highest speed, his acceleration must be zero and so this much occurat the same level as the final equilibrium position (l=l2)
Again applying the law of conservation of energy
12mv2+12k(l2−l0)2=mg(l2+h0)
where the ratio m//k is the same as that obtained from the equilibrium condition, namely
mk=l2−l0g
Substituting this into the energy equation, shows that the maximum speed of the jumper is v=18ms−1≈65kmh−1 It is easy to see that his maximum acceleration occurs at the lowest point of the jump Since the largest extension of the rope (10m) is five times that at the equilibrium position (2m), the greatest tension in the rope is 5 mg So the highest net force exerted on the jumper is 4 mg and his maximum acceleration is 4g.
Topper's Solved these Questions
- MASTER PRACTICE PROBLEMBOOK - BANSALCHAPTER - MASTER PRACTICE PROBLEMEXERCISE - Additional topic
70 Videos
- MASTER PRACTICE PROBLEMBOOK - BANSALCHAPTER - MASTER PRACTICE PROBLEMEXERCISE - Multiple objective
131 Videos
- FLUID MECHANICSBOOK - BANSALCHAPTER - FLUID MECHANICSEXERCISE - PYQS AIEEE
10 Videos
- SEMICONDUCTORSBOOK - BANSALCHAPTER - SEMICONDUCTORSEXERCISE - CBSE Question
32 Videos
Similar Questions
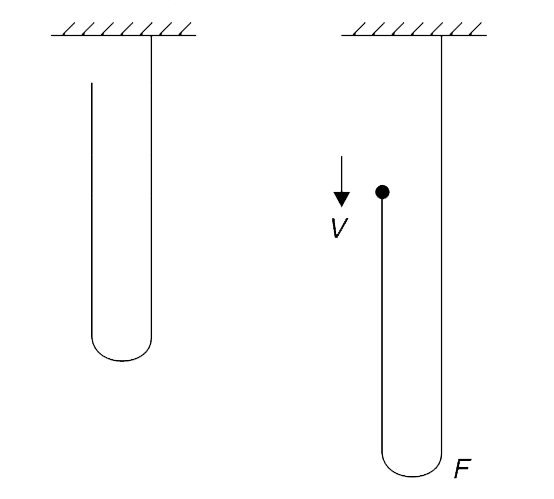
One end of a rope is fixed at a point on the ceiling the other end is held close to the first end so that the rope is folded. The second end is released from this position. Find the speed at which the fold at F is descending at the instant the free end of the rope is going down at speed V.
View SolutionA man of mass m stands on a frame of mass M. He pulls on a light rope, which passes over a pulley. The other end of the rope is attached to the frame. For the system to be in equilibrium, what force must the man exert on the rope?

View Solution
Knowledge Check
A block of mass 2m is hanging at the lower and of a ropeof mass m and length the l, the other end being fixed to the ceililng. A pulse of wavelength λ0 is produced at the lower of the rope.
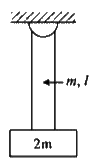
The speed of the pulseat the mid point of rope is:A√52glB√33glC√25glD√gl2A ladder is resting with one end is contact with the top of a wall of height 60 m and the other end on the ground is at a distance of 11 m form the wall. The length of the ladder is :
A61 mB71 mC87 mDnone of theseA man of mass m stands on a frame of mass M. He pulls on a light rope, which passes over a pulley. The other end of the rope is attached to the frame. For the system to be in equilibrium, what force must the man exert on the rope?
 A(M+m)g2B(M+m)gC(M−m)gD(M+2m)g
A(M+m)g2B(M+m)gC(M−m)gD(M+2m)g
A rope from the top of a mast on a sailboat is attached to a point 2 m from the base of the mast. The rope is 8 m long. What is the height of the mast?
View SolutionA ball of mass m strikes the fixed inclined plane after falling through a height h. if it rebounds elastically. The impulse on the ball is :
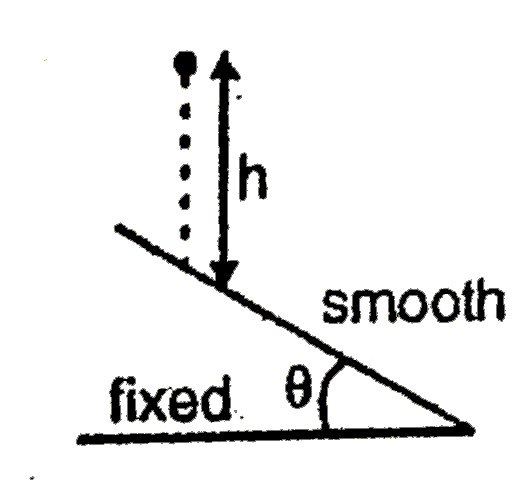
View SolutionA ball of mass m strikes the fixed inclined plane after falling through a height h. if it rebounds elastically. The impulse on the ball is :
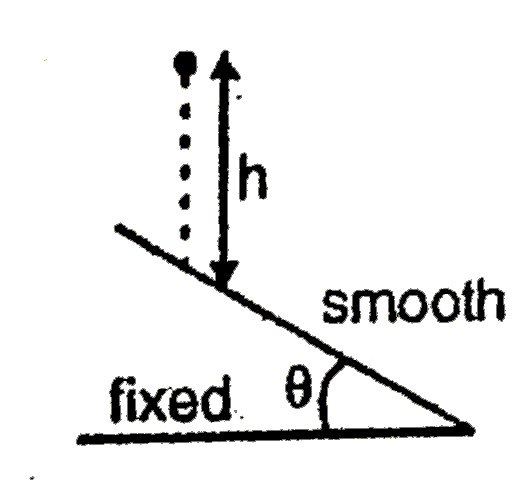
View SolutionA uniform rod of length L and weight W is suspended horizontally by two vertical ropes as shown. The first rope is attached to the left end of the rod while the second is attached to the left end of the rod while the second rope is attached a distance L/4 from the right end. The tension in the second rope is.
 .
.
View SolutionA man of 2 m height walks at a uniform speed to 6 km/h, away from a lamp post of 6 m height. The rate at which the length of his shadow increase is
View Solution
