If the kinetic energy of pulse travelling in a taut string is K×10−2 mJ then find the value of K (Given T=10N&μ=0.1kg/m
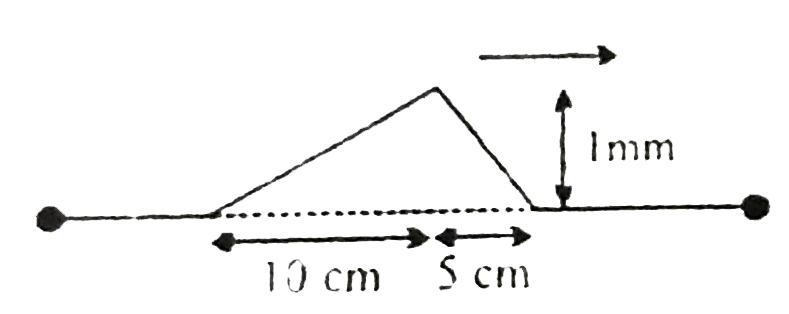
The correct Answer is:15
at given time y=m1x0<x<0.1 m
=m2x+C0.1m<x<0.15 m
m1=10−30.1=10−2(Vω=√Tμ)
m2=10−30.05=2×10−2
dK=12dmV2p=12μdx(−Vω∂y∂x)2
∫dK=12μV2ω⎡⎢⎣m210.1∫0dx+m220.15∫0.1dx⎤⎥⎦
K=12T[m21(0.1)+m22(0.5)]
K=12T[10−4(0.1)+4×10−4(0.5)]
=102[10−4](0.3)=0.15mJ

Topper's Solved these Questions
- MASTER PRACTICE PROBLEMBOOK - BANSALCHAPTER - MASTER PRACTICE PROBLEMEXERCISE - Additional topic
70 Videos
- MASTER PRACTICE PROBLEMBOOK - BANSALCHAPTER - MASTER PRACTICE PROBLEMEXERCISE - Multiple objective
131 Videos
- FLUID MECHANICSBOOK - BANSALCHAPTER - FLUID MECHANICSEXERCISE - PYQS AIEEE
10 Videos
- SEMICONDUCTORSBOOK - BANSALCHAPTER - SEMICONDUCTORSEXERCISE - CBSE Question
32 Videos
Similar Questions
The kinetic energy of 1 kg of oxygen at 300 K is 1.169×105 J . Find the kinetic energy of 2 kg of oxygen at 500 K.
View SolutionAn 80 kg person is parachuting and is experiencing a downward acceleration of 2.8 m s−2. The mass of the parachute is 5 kg. If the upward force on the open parachute is k×102N, then what is the value of k? (Take g=9.8ms−2)
View Solution
Knowledge Check
A string of length 0.4 m and mass 10−2 kg is clamped at its ends. The tension in the string is 1.6 N. When a pulse travels along the string the shape of the string is found to be the same at times t and t+△t. The value △t is
A0.05sB0.1sC0.2sD0.4s
An 80 kg person is parachuting and is experiencing a downward acceleration of 2.8 m s−2. The mass of the parachute is 5 kg. If the upward force on the open parachute is k×102N, then what is the value of k? (Take g=9.8ms−2)
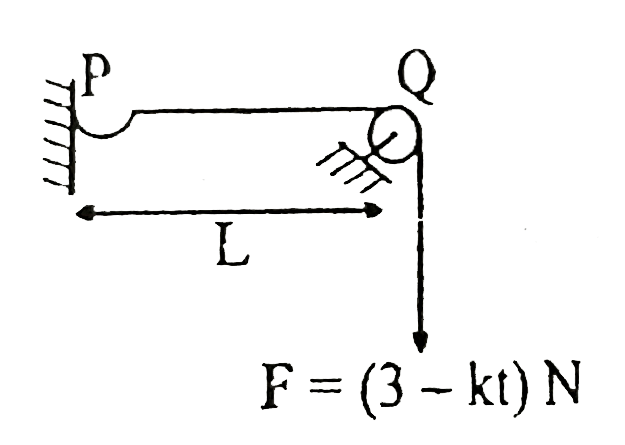
View SolutionIn the given figure a string of linear mass density 3×10−2 kg//m and length L=1 m, is stretched by a froce F=(3−kt)N, where k is a constant and t is time in sec. At the time t=0, a pulse is generated at the end P of the string Find the value of k (in N//s) if the value of force becomes zero as the pulse reaches point Q.
View SolutionFind the kinetic energy of a body of mass 1 kg moving with a uniform velocity of 10 ms−1
View SolutionIf the sum 10∑n=110∑m=1tan−1(mn)=kπ, find the value of k
View SolutionA wave pulse starts propagating in the x direction along a non uniform wire of length 10m with mass per unit length is given by μ=μ0+ax and under a tension of 100N. The time taken by a pulse to travel from the lighter end to heavier end (μ0=10−2kg/m and a=9×10−3kg/m2) is
View SolutionA wave pulse starts propagating in the x direction along a non uniform wire of length 10m with mass per unit length is given byμ=μ0+ax and under a tension of 100N. The time taken by a pulse to travel from the lighter end to heavier end (μ0=10−2kg/m and a=9×10−3kg/m2) is
View SolutionA wave pulse starts propagating in the +x-direction along a non-uniform wire of length 10 m with mass per unit length given by μ=μ0+az and under a tension of 100 N. find the time taken by a pulse to travel from the lighter end (x=0) to the heavier end. (mu_(0)=10^(2) kg//m and a=9xx10^(-3)kg//m^(2)).
View Solution
