A tiny electric dipole of dipole moment p is palced at a distance r from an infinitely long wire, with its →p normal to the wire. If the linear charge density of the wire is λ, the electrostatic force acting on the dipole is equal to
λP4πε0r
λPπε0r
2λPπε0r
λP2πε0r2
λp2πε0r2
Fnet=2Fsin(θ/2)
=Fθ=qE(l/r)
=λp2πε0r2

Topper's Solved these Questions
- GMP ASSESMENTBOOK - FIITJEECHAPTER - GMP ASSESMENTEXERCISE - Assertion & Reason
15 Videos
- GMP ASSESMENTBOOK - FIITJEECHAPTER - GMP ASSESMENTEXERCISE - Multiple Question
58 Videos
- GMP ASSESMENTBOOK - FIITJEECHAPTER - GMP ASSESMENTEXERCISE - Numerical Based
61 Videos
- GENERAL PHYSICSBOOK - FIITJEECHAPTER - GENERAL PHYSICSEXERCISE - MATRIX MATCH TYPE
3 Videos
- GRAVITATIONBOOK - FIITJEECHAPTER - GRAVITATIONEXERCISE - Numerical based Question
2 Videos
Similar Questions
An electric dipole of moment p is kept at a distance r form an infinte long charged wire of linear charge density λ as shown.Find the force acting on the dipole?

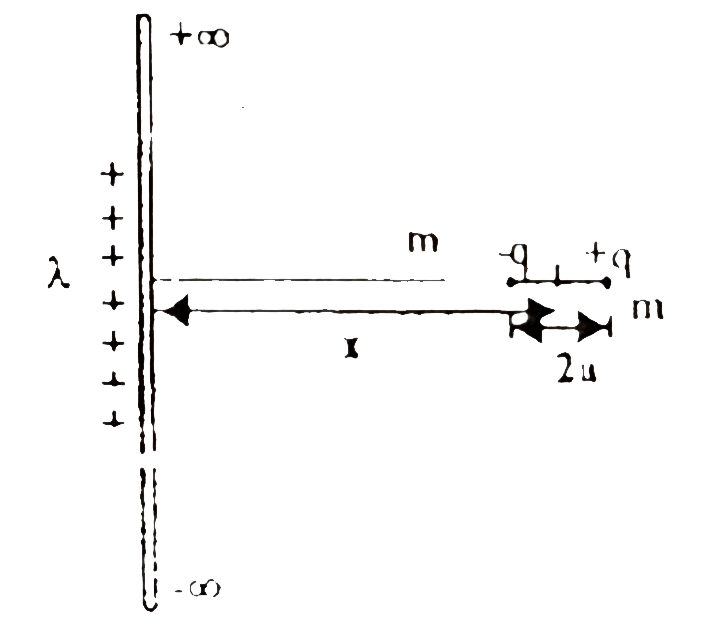
View SolutionIn the figure shown, an electric dipole is placed at a distance x from an infinitely long rod of linear charge density λ.
(a) Find the net force acting on the dipole ?
(b) What is the work done in rotating the dipole through 180∘ ?
(c) If the dipole is slightly rotated about its equilibrium position, find the time period of oscillation. Assume that the dipole is linearly restrained.
View Solution
Knowledge Check
A small electric dipole of dipole moment P is placed at a distance r from one infinitely long uniformly charged, straight conductor. If λ is the linear charge density of straight conductor and axis of the dipole is perpendicular to the straight conductor then the force acting on the dipole is
AλP2πε0r2BλP2πε0rCλP4πε0r2DλPπε0r2An infinitely long wire with linear charge density +λ is bent and the two parts are inclined at angle 30∘ as shown in fig, the electric field at point P is :
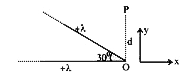 Aλ4π∈0d[(1+√3)ˆi+ˆj]Bλ4π∈0d[(1−√3)ˆi+2ˆj]Cλ4π∈0d[(1+√3)ˆi−2ˆj]Dλ4π∈0d[(1+√3)ˆi+2ˆj]
Aλ4π∈0d[(1+√3)ˆi+ˆj]Bλ4π∈0d[(1−√3)ˆi+2ˆj]Cλ4π∈0d[(1+√3)ˆi−2ˆj]Dλ4π∈0d[(1+√3)ˆi+2ˆj]A charge particle q is released at a distance R∘ from the infinite long wire of linear charge density λ. Then velocity will be proportional to (At distance R from the wire)
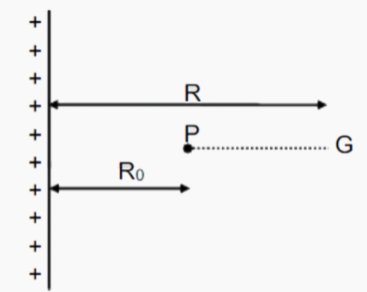 AR3BeR/R0CR2D[n(RR0)]−1/2
AR3BeR/R0CR2D[n(RR0)]−1/2
In figure-, an electric dipole is placed at a distance x from an infinitely long rod of linear charge density λ.
(a) Find the net force acting on the dipole
(b) What is the work done in rotating the dipole through 180∘
(c ) If the dipole is slightly rotated about its equilibrium position, find the time period of oscillation. Assume that the dipole is linearly restrained.
[(a)λaqπ∈0x2,(b)2λaqπ∈0x,(c)2π√2π∈0mx2aλq]

View SolutionIn the figure shown, an electric dipole is placed at a distance x from an infinitely long rod of linear charge density λ.
(a) Find the net force acting on the dipole ?
(b) What is the work done in rotating the dipole through 180∘ ?
(c) If the dipole is slightly rotated about its equilibrium position, find the time period of oscillation. Assume that the dipole is linearly restrained.

View SolutionA short electric dipole has dipole moment p. Find the distance of farthest point from the dipole where (a) potential due to the dipole is V0 (b) Electric field due to the dipole is E0
View SolutionA very small electric dipole with dipole moment p is placed in such in way that it is at a distance r from another point charge +q. The point charge lies on the axis of the dipole . Electric dipole moment is pointing towards the point charge. Determine electric dipole will attract the point charge or repel it ? What will be the magnitude of force between them ?
View SolutionAn infinitely long wire with linear charge density +λ is bent and the two parts are inclined at angle 30∘ as shown in fig, the electric field at point P is :

View Solution
