In the figure shown, an electric dipole is placed at a distance x from an infinitely long rod of linear charge density λ.
(a) Find the net force acting on the dipole ?
(b) What is the work done in rotating the dipole through 180∘ ?
(c) If the dipole is slightly rotated about its equilibrium position, find the time period of oscillation. Assume that the dipole is linearly restrained.
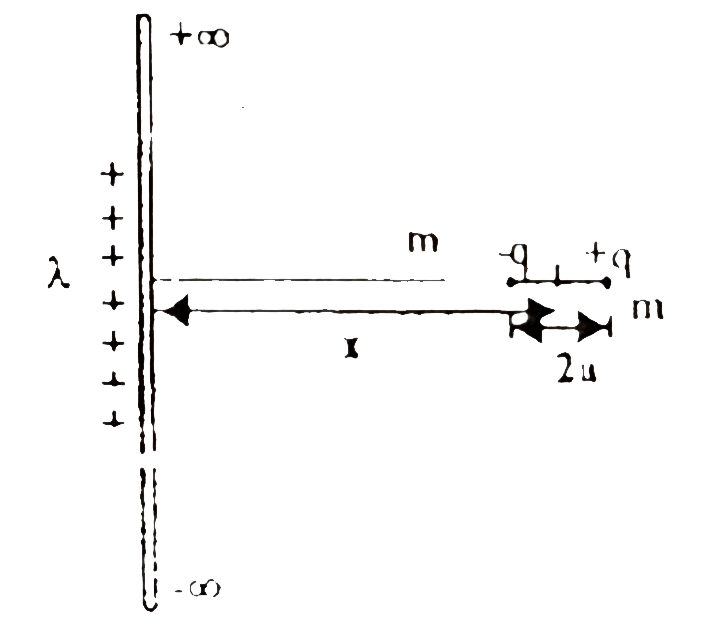
(a) The electric field at a distance x is
E=λ2πε0x
The net force on the dipole is
F=pdEdx=(2a)q[−λ2πε0x2]=−λqaπε0x2
The negative sign indicates that the force is attractive.
(b) W=ΔU
Ui=−→p⋅→E=−pEcos0∘=−pE
Uf=−→p⋅→E=−pEcos180∘=+pE
W=2pE=2(2a)qλ2πε0x=2λqaπε0x
(c) Restoring torque
τ=−pEsinθ
τ=Id2θdt2=(2ma2)d2θdt2
∴2ma2d2θdt2+[λqaπε0x]θ=0
or d2θdt2+[λq2πε0max]θ=0
T=2π√2πε0maxλq=√8π2ε0maxλq
Topper's Solved these Questions
- GMP ASSESMENTBOOK - FIITJEECHAPTER - GMP ASSESMENTEXERCISE - Objective problems
215 Videos
- GMP ASSESMENTBOOK - FIITJEECHAPTER - GMP ASSESMENTEXERCISE - Assertion & Reason
15 Videos
- GENERAL PHYSICSBOOK - FIITJEECHAPTER - GENERAL PHYSICSEXERCISE - MATRIX MATCH TYPE
3 Videos
- GRAVITATIONBOOK - FIITJEECHAPTER - GRAVITATIONEXERCISE - Numerical based Question
2 Videos
Similar Questions
In figure-, an electric dipole is placed at a distance x from an infinitely long rod of linear charge density λ.
(a) Find the net force acting on the dipole
(b) What is the work done in rotating the dipole through 180∘
(c ) If the dipole is slightly rotated about its equilibrium position, find the time period of oscillation. Assume that the dipole is linearly restrained.
[(a)λaqπ∈0x2,(b)2λaqπ∈0x,(c)2π√2π∈0mx2aλq]

View SolutionAn electric dipole of moment p is kept at a distance r form an infinte long charged wire of linear charge density λ as shown.Find the force acting on the dipole?

View Solution
Knowledge Check
The work done in deflecting a dipole through 180∘ from field direction is
Aperpendicular to each otherB2PEC12PEDzeroAs shown in the figure an electric dipole lies at a distance x from the centrr of a chargerd ring of radius R with charge Q uniformly distributed over it .The net force acting on the dipole is
 AaQq4πε0R2−2x22πε0(R2+x2)5/2BaQq2πε0R2+2x22πε0(R2+x2)5/2CaQq4πε0R2+2x22πε0(R2+x2)5/2DaQq2πε0R2−2x22πε0(R2+x2)5/2
AaQq4πε0R2−2x22πε0(R2+x2)5/2BaQq2πε0R2+2x22πε0(R2+x2)5/2CaQq4πε0R2+2x22πε0(R2+x2)5/2DaQq2πε0R2−2x22πε0(R2+x2)5/2A tiny electric dipole of dipole moment p is palced at a distance r from an infinitely long wire, with its →p normal to the wire. If the linear charge density of the wire is λ, the electrostatic force acting on the dipole is equal to
AλP4πε0rBλPπε0rC2λPπε0rDλP2πε0r2
An electric dipole is placed at a distance x from centre O on the axis of a charged ring of R and charge Q uniformly distributed over it.
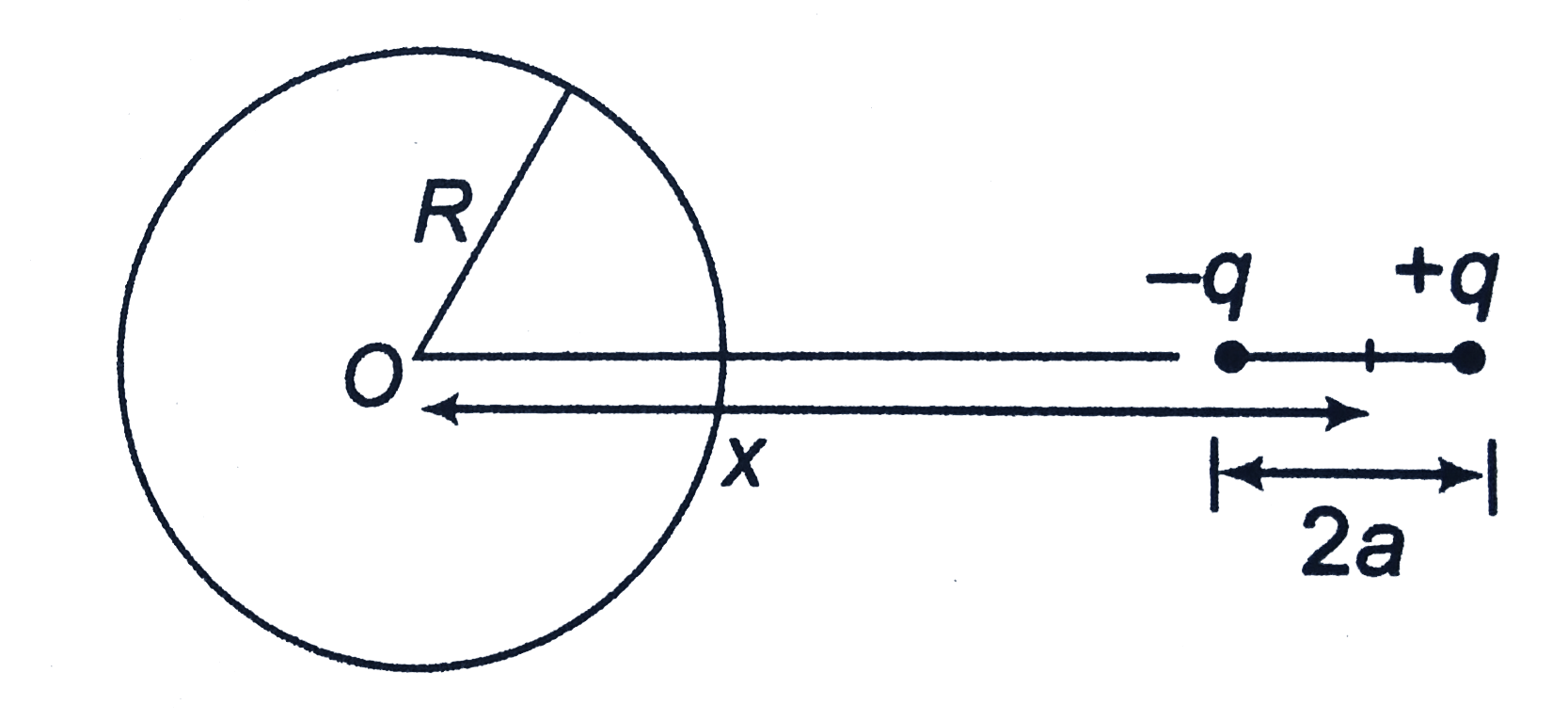
(a) Find the net force acting on the dipole.
(b) What is the work done in rotating the dipole through 180∘?
View SolutionNet charge on an electric dipole is ………….. .
View SolutionA dipole with an electric moment p is located at a distance r from a along thread charge uniformly with a linear density λ. Find the force F acting on the dipole if the vector p is oriented
(a) along the thread
(b) along the radius vector r
(c ) at the right angles to the thread and the radius vector r.
View SolutionAn electric dipole is held in a uniform electric field.
(i) Show that the net force acting on it is zero.
(ii) The dipole is aligned parallel to the field. Find the work done in rotating it through the angle of 180∘.
View SolutionAn electric dipole is placed perpendicular to an infinite line of charge at same distance as shown in figure. Identify the correct statement.

View Solution
