A particle A is moving in xy plane with the constant speed of 2πm/s along the path x2+y2+120y=0. At time t=0. When A is at the origin, another particle B starts moving from origin with constant acceleration is such a way that at time t=5s velocities of both the particles are found to be equal. If sense of motion of A is clockwise, calculate the average speed of B over first five second.
2πm/s
πm/s
2m/s
1m/s
60θ=10π
θ=π/6
→VA=−v0cos30∘ˆi−v0sin30∘ˆj
=−v02[√3ˆi+ˆj]
⇒→VB=→VA=−V02[√3ˆi+ˆj]
→aB=−V02[√3ˆi+ˆj]
Since particle starts moving with uniform acceleration so it will move on a straight line
→SB=→UBt+12→aBt2=0+V020[√3ˆi+ˆj]×25
∣∣→SB∣∣= Distance travelled by particle B=2π20×25×2=5π
Average speed of particle B over first five second 5π5=πm/s
Second method
∵→aB=constant, to
0<VB<5sec=∣∣
∣∣→VB(a)+→VB(5)2∣∣
∣∣=V02=πm/s

Topper's Solved these Questions
- GMP ASSESMENTBOOK - FIITJEECHAPTER - GMP ASSESMENTEXERCISE - Assertion & Reason
15 Videos
- GMP ASSESMENTBOOK - FIITJEECHAPTER - GMP ASSESMENTEXERCISE - Multiple Question
58 Videos
- GMP ASSESMENTBOOK - FIITJEECHAPTER - GMP ASSESMENTEXERCISE - Numerical Based
61 Videos
- GENERAL PHYSICSBOOK - FIITJEECHAPTER - GENERAL PHYSICSEXERCISE - MATRIX MATCH TYPE
3 Videos
- GRAVITATIONBOOK - FIITJEECHAPTER - GRAVITATIONEXERCISE - Numerical based Question
2 Videos
Similar Questions
A particle of mass m is moving along the line y-b with constant acceleration a. The areal velocity of the position vector of the particle at time t is (u=0)
View SolutionA particle is kept at rest at the origin. A constant force →F starts acting on it at t=0. Find the speed of the particle at time t.
View Solution
Knowledge Check
A particle of mass m is moving along the line y-b with constant acceleration a. The areal velocity of the position vector of the particle at time t is (u=0)
AconstantBabt2Cabt2mDa2bt2mA particle moves in a circle of radius 5 cm with constant speed and time period 0.2πs. The acceleration of the particle is
A25ms−2B36ms−2C5ms−2D15ms−2A particle moves in a circle of radius 5 cm with constant speed and time period 0.2πs. The acceleration of the particle is
A25m/s2B36m/s2C5m/s2D15m/s2
A particle starts from the origin at t = 0 s with a velocity of 10.0ˆj m/s and moves in plane with a constant acceleration of (8ˆi+2ˆj)ms−2. The y-coordinate of the particle in 2 sec is
View SolutionA particle confined to motion along an x axis moves with constant acceleration from x=2.0m to x=8.0 m during a 2.5 s time interval. The velocity of the particle at x=8.0m is 2.8 m/s. What is the constant acceleration during this time interval ?
View SolutionA particle moves in a circle of radius 5 cm with constant speed and time period 0.2πs. The acceleration of the particle is
View SolutionA particle moves in the x-y plane with a constant acceleration of 1.5m/s2 in the direction making an angle of 37∘ with the x-axis.
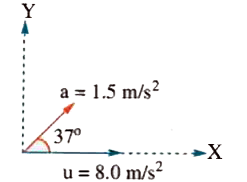
At t=0 the particle is at the origin and its velocity is 8.0m/s along the x- aixs . Find the velocity and the position of the particle at t = 4.0s.
View SolutionA particle starts from the origin at t=Os with a velocity of 10.0ˆjm/s and moves in the xy-plane with a constant acceleration of (8ˆi+2ˆj)m/s−2. What time is the x-coordinate of the particle 16m?
View Solution
