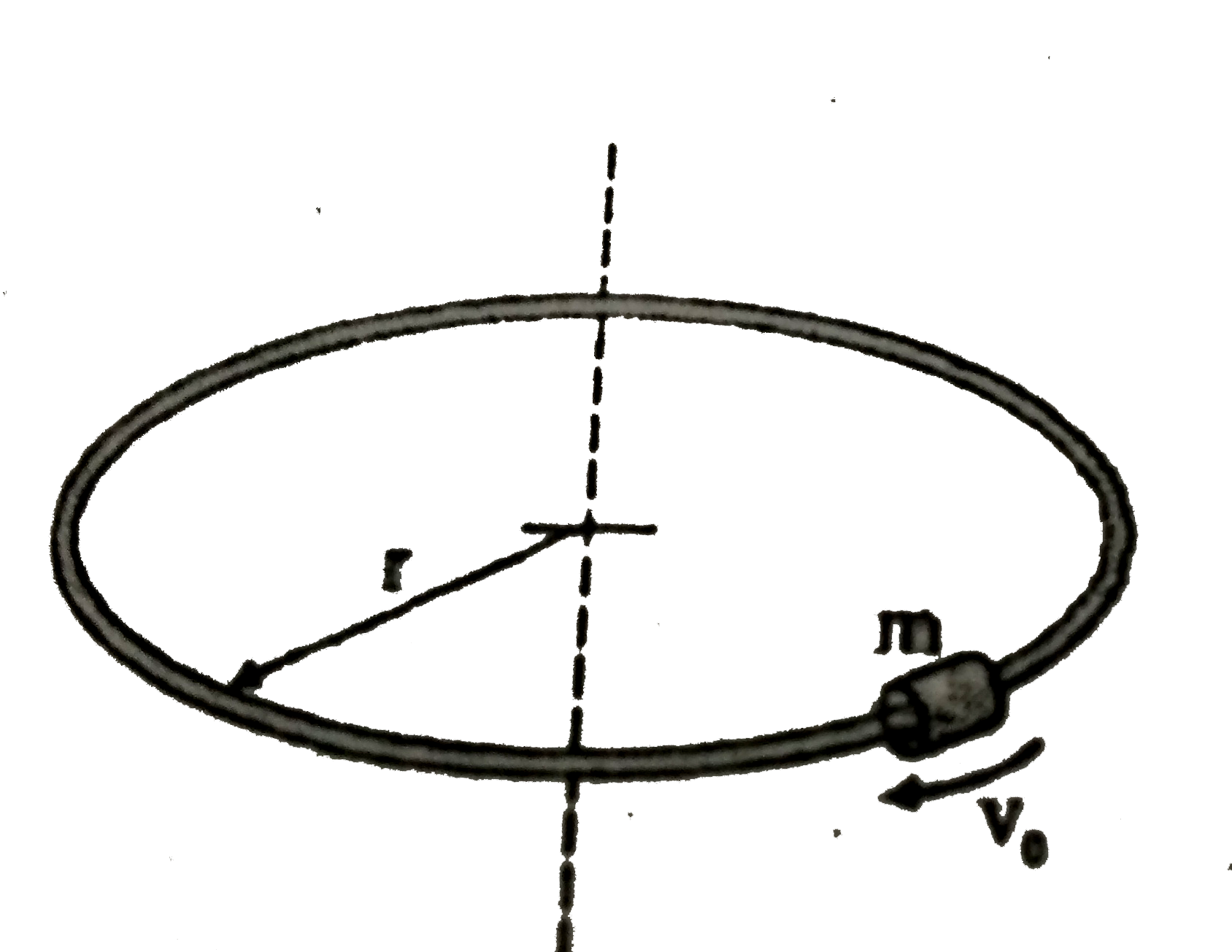
A small collar of mass m is given an intial velocity of magnitude v0 on the horizontal circular track fabricated from a slender rod. If the coefficient of kinetic friction is μK, determine the distance travelled before the collar comes to rest. (Recognize that the friction force depends on the net normal force).

rμkln⎡⎢ ⎢⎣v20+√v40+r2g2rg⎤⎥ ⎥⎦
r4μkln⎡⎢ ⎢⎣v20+√v40+r2g2rg⎤⎥ ⎥⎦
2rμkln⎡⎢ ⎢⎣v20+√v40+r2g2rg⎤⎥ ⎥⎦
r2μkln⎡⎢ ⎢⎣v20+√v40+r2g2rg⎤⎥ ⎥⎦
−μN=ma
−μ√mv2r+(mg2)=ma
⇒a=−μ√v4r2+g2
⇒dvdxdxdt=−μ√v4r2+g2
⇒Let v2r=t⇒2vdvr=dt
⇒∫r2dt√t2+g2=−μ∫dx
⇒r2{ln(t+√t2+g2)}=−[μx]s0
⇒r2{ln(v2r+√v2r2+g2)}0v0=−μ[x]s0
⇒S=r2μln⎡⎢
⎢⎣v20+√v40+r2g2rg⎤⎥
⎥⎦
Topper's Solved these Questions
- BOOK - FIITJEECHAPTER - GMP ASSESMENTEXERCISE - Assertion & Reason15videos
GMP ASSESMENT
- BOOK - FIITJEECHAPTER - GMP ASSESMENTEXERCISE - Multiple Question58videos
GMP ASSESMENT
- BOOK - FIITJEECHAPTER - GMP ASSESMENTEXERCISE - Numerical Based61videos
GMP ASSESMENT
- BOOK - FIITJEECHAPTER - GENERAL PHYSICSEXERCISE - MATRIX MATCH TYPE3videos
GENERAL PHYSICS
- BOOK - FIITJEECHAPTER - GRAVITATIONEXERCISE - Numerical based Question2videos
GRAVITATION
Similar Questions
A small bead of mass m is given an initial velocity of magnitude v0 on a horizontal circular wire. If the coefficient of kinetic friction is μk, determine the distance travelled before the collar comes to rest.
View SolutionA small bead of mass m is given an initial velocity of magnitude v0 on a horizontal circular wire. If the coefficient of kinetic friction is μk, determine the distance travelled before the collar comes to rest.
View Solution
Knowledge Check
- Question 1 - Select One
A small hoop of mass m is given an initial velocity of magnitude v0 on the horizontal circular ring of radius 'r'. If the coefficient of kinetic friction is μk the tangential acceleration of the hoop immediately after is release is ( assume the horizontal ring to be fixed and not in contact with any supporting surface )
 AμkgBμkv20rCμk√g2+v2rDμk√g2+v0r2
AμkgBμkv20rCμk√g2+v2rDμk√g2+v0r2 - Question 2 - Select One
A body is given a velocity √2gr at the highest point of a half circular smooth track which is joined by a rough horizontal track whose co− efficient of friction is μ=0.5. Then the distance travelled by particle before it stops on horizontal track is :(r=1m)
 A1mB4mC6mDnone of these
A1mB4mC6mDnone of these - Question 3 - Select One
A ring of mass m sliding on a smooth surface with velocity v0 enters rough surface with coefficient of kinetic friction μk, then
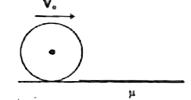 Athe linear distance moved by centre of mass before the ring starts pure rolling is 3v208μkgBthe gain in kinetic energy is mv208Cthe loss in kinetic energy is mv204Dthe work done by friction force is −3mv208
Athe linear distance moved by centre of mass before the ring starts pure rolling is 3v208μkgBthe gain in kinetic energy is mv208Cthe loss in kinetic energy is mv204Dthe work done by friction force is −3mv208
A block is projected along a rough horizontal road with a speed of 10 m/s. If the coefficient of kinetic friction is 0.10, how far will it travel before coming to rest?
View SolutionA block of mass m moving with a velocity v0 on a rough horizontal surface from x=0 coefficient of friction is given by μ=μ0=ax. Find the kinetic energy of the block as function of x before it comes to rest.
View SolutionOne end of a light string is slipped around a peg fixed in a horizontal table top, while the other end is tied to a 0.5 kg small disc. The disc is given an initial velocity of magnitude 3.4m/s so that it moves in a horizontal circle of radius 0.75 m. The object comes to rest after 2.5 revolutions (a) For the entire motion, what work is done by the frictional force ? (b) Assume that the magnitude of the frictional force is constant and determine the coefficient of kinetic friction at the interface (c) Determine the tension in the string at the instant that the disc completes the first revolution (d) How much work is done by the tension in the string ?
View SolutionA small mass slides down an inclined plane of inclination θ the horizontal the coefficient of friction is m=μ0x, where x is the distance by the mass before it stops is .
View SolutionA block of mass M is using on a rough horizontal surface. μR is the coefficient of kinetic friction between the block and the surface. What is the net force exerted by the surface on the block?
View Solution

