Question

A string fixed at both ends is vibrating such that a point at quarter of its length from one end is a point of maximum displacement. The frequency of vibration in this mode is ${\displaystyle 100Hz}$. If the frequency emitted when it vibrates in the next mode such that this point is again a point of maximum displacement is ${\displaystyle 100k}$ then find the value of ${\displaystyle k}$.

Explanation

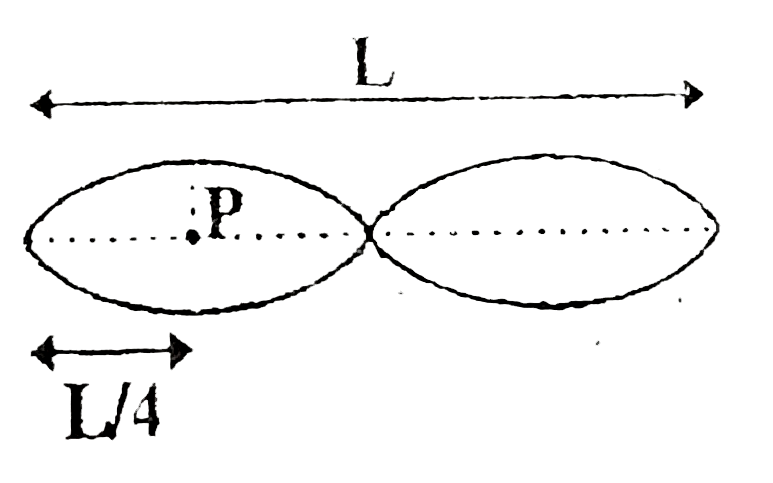
The figure rerpesents the mode of vibration for which frequency is `100 Hz`.
Here, `L=lambda`
In the next higher mode with `P` again an anti-node, for every `L//4` length, there will be one extra loop. Thus for the total string, total number of loops `=6`
`rArr ` Desired frequency `=(6//2)100Hz=300Hz`