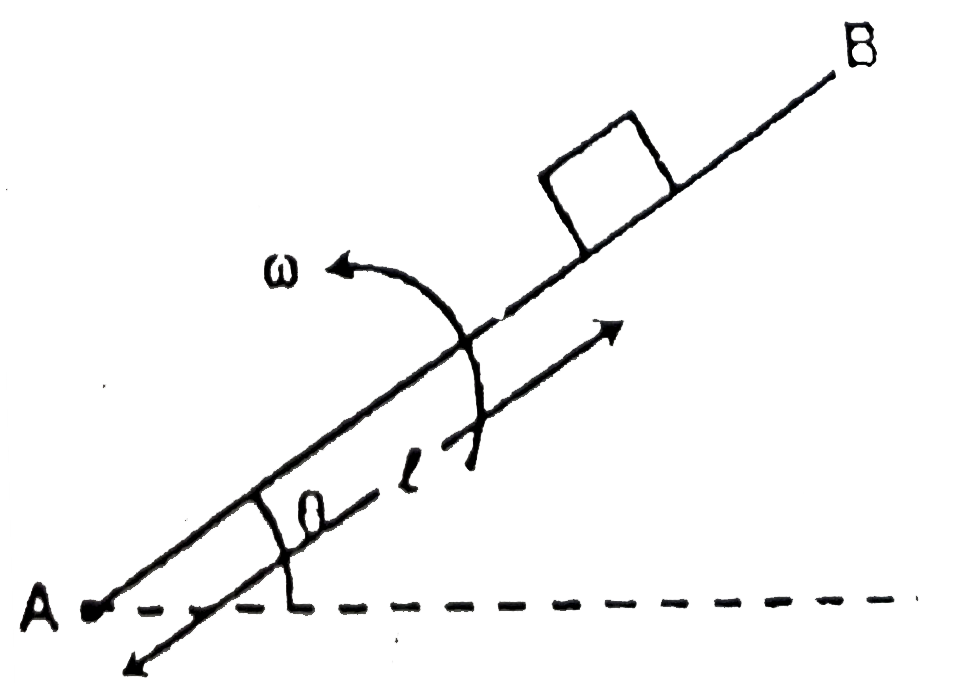
A plank is rotating in a vertical plane about one of its ends with a constant angular velocity ω=√2rad/s. A block of mass m=2kg is placed at a distance l=1m from its end A (see figure) which is hinged. The block starts sliding down when the plank makes an angle θ=30∘ with the horizontal. If coefficient of friction between the plank and the block is μ and given that μ2=k/25. Find the value of k.
1v−1u=1f
v−u=x,
1u+x−1u=1f
⇒1u+x=1u+1f
u+x=ufu+f
x=ufu+f−u=u[fu+f−1]
x=−u2u+f
differentiating w.r.t. x,
∴δx=[−2uu+f+u2(u+f)2]δu
=−2u(u+f)+u2(u+f)2δu
=−u2+2uf(u+f)2δu
δx=(u+f)2+f2(u+f)2=[(fu+f)−1]δu
δu=a<<|u|=|3f|
δx=[(f−3f+f)2−1]a=−34a
Amplitude =|δx|=34a
Topper's Solved these Questions
Similar Questions
A block of mass m slides down an inclined plane which makes an angle θ with the horizontal. The coefficient of friction between the block and the plane is μ. The force exerted by the block on the plane is
View SolutionA block slides down an inclined plane that makes an angle θ with the horizontal. If the coefficient of kinetic friction is μ, find the acceleration of the block.
View Solution
Knowledge Check
A block of mass m slides down an inclined plane which makes an angle θ with the horizontal. The coefficient of friction between the block and the plane is μ. The force exerted by the block on the plane is
AmgcosθB√μ2+1mgcosθCμmgcosθ√μ2+1DμmgθA block of mass m is placed on a rough plane inclined at an angle θ with the horizontal. The coefficient of friction between the block and inclined plane is μ . Ifθ<tan−1(μ) , then net contact force exerted by the plane on the block is :
Amg cos θBmgCmg sin θDNone of theseA block of mass m=2kg is placed in equilibrium on a moving plank accelerating with a=1m/s2 . If coefficient of friction between plank and block μ=0.2 . The friction force acting on theblock is:
A2NB4NC3NDNone of these
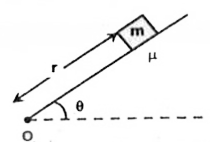
A small block of mass m is placed at a distance r from one end of a plank. The plank is given a constant angular velocity ω about an axis passing through point O and perpendicular to the plane. The block starts sliding down the plane when the plank makes an angle θ with horizontal. Calculate the coefficient of friction between the particle and the plank.
View SolutionA block of mass m is placed on a rough plane inclined at an angle θ with the horizontal. The coefficient of friction between the block and inclined plane is μ . Ifθ<tan−1(μ) , then net contact force exerted by the plane on the block is :
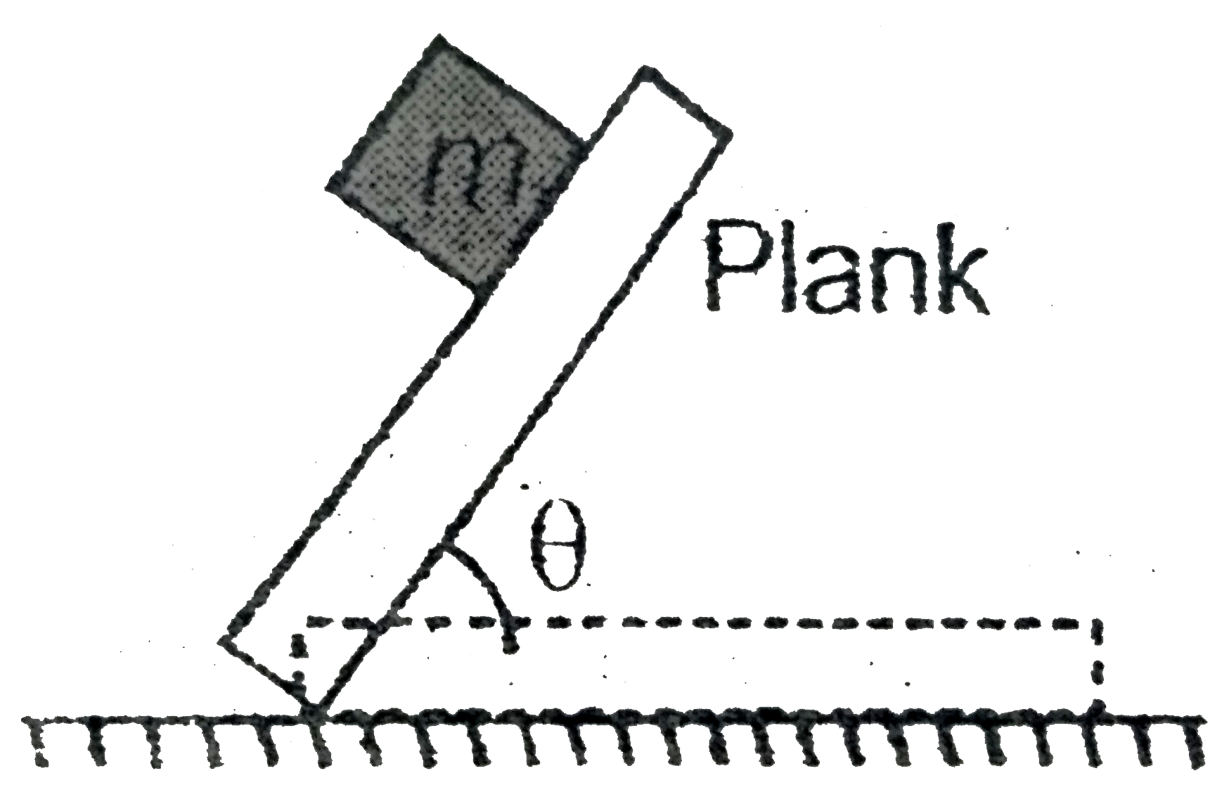
View SolutionA block of mass m is kept on a plank . The coefficient of friction between the plank and block is 1. The plank is slowly raised from one end so that it makes angle θ with horizontal . The forces of friction acting on the plank , when θ=30∘andθ60∘ are respectively,
View SolutionA block of mass 2 kg slides down an incline plane of inclination 30°. The coefficient of friction between block and plane is 0.5. The contact force between block and plank is :
View SolutionA block of mass m=2kg is placed in equilibrium on a moving plank accelerating with a=4m/s2 . If coefficient of friction between plank and block μ=0.2 . The friction force acting on the block is:
View Solution
