A block of mass m rigidly attached with a spring k is compressed through a distance A. If the block is released, the period of oscillation of the block for a complete cycle is equal to

4π3√mk
π√2√mk
2π3√mk
None of these
The period of motion from A to O is equal to quarter of the time period T of oscillation of mass spring system.
⇒tAO=T4=14[2π√mk]=π2√mk
Since the motion is simple harmonic
OB=OAsin2πTtOB, where tOB is the time of motion from O to B.
⇒tOB=T2πsin−1A/2A=T2π(π6)
=T12=2π12√mk=π6√mk
∴ The total time of motion for a complete cycle =t=2(tAO+tOB)
⇒t=2[π2√mk+π6√mk]=4π3√mk.
Topper's Solved these Questions
Similar Questions
A block of mass m compresses a spring iof stifffness k through a distacne l/2 as shown in the figure .If the block is not fixed to the spring the period of motion of the block is

View SolutionA block of mass 'm' is attached to a spring. Block is released from rest, when spring is in natural length. Block is along the pricipal axis of concave mirror and size of block is very small. When spring is in natural length then block is at a distance of 20 cm from the mirror, distance (in cm) in which the image formed by mirror oscillates is (mass of the block =5×10−2 kg, spring constant k=20 N//m)

View Solution
Knowledge Check
Calculate the period of oscillations of block of mass m attached with a set of springs as shown
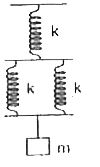 A2π√m3kB2π√3m2kC2π√2m3kD2π√3km
A2π√m3kB2π√3m2kC2π√2m3kD2π√3kmA block of mass m compresses a spring iof stifffness k through a distacne l/2 as shown in the figure .If the block is not fixed to the spring the period of motion of the block is
 A2π√mkB(π+4)√mkC(1+π)√mkDNone of these
A2π√mkB(π+4)√mkC(1+π)√mkDNone of theseIn the figure, the block of mass m, attached to the spring of stiffness k is in correct with the completely elastic wall, and the compression in the spring is e. The spring is compressed further by e by displacing the block towards left and is then released. If the collision between the block and the wall is completely eleastic then the time period of oscillation of the block will be
 A2π3)√mkB(2π)√mkCπ3√mkDπ6√mk
A2π3)√mkB(2π)√mkCπ3√mkDπ6√mk
In the figure, the block of mass m, attached to the spring of stiffness k is in correct with the completely elastic wall, and the compression in the spring is e. The spring is compressed further by e by displacing the block towards left and is then released. If the collision between the block and the wall is completely eleastic then the time period of oscillation of the block will be

View SolutionA block of mass m is attached to a cart of mass 4m through spring of spring constant k as shown in the figure. Friction is absent everywhere. The time period of oscillations of the system, when spring is compressed and then released, is

View Solution
A block of mass m is attached to two unstretched springs of spring constant k, each as shown. The block is displaced towards right through a distance x and is released The speed of the block as it passes through the mean position will be
View SolutionFigure shown a block P of mass m resting on a smooth horizontal surface, attached to a spring of force constant k which is rigidly fixed on the wall on left side, shown in the figure . At a distance l to the right of the block there is a rigid wall. If block is pushed towards left so that spring is compressed by a distance 5l/3 and when released, if will starts its oscillations. If collision of block with the wall is considered to be perfectly elastic. Find the time period of oscillation of the block.

View Solution
A block of mass m is attached to two unstretched springs of spring constant k, each as shown. The block is displaced towards right through a distance x and is released The speed of the block as it passes through the mean position will be
View Solution
