Time period of a block when suspended from the upper plate of a parallel plate capactor by a spring of stiffness k is when block ids unchanged If a change g is given to the block then new time period of oscilation will be

T
>T
<T
≥T
The forces that act on the block are qE and mg. Since qE and mg are constant forces, the only variable elastic force changes by kx, where x is the elongation in the spring
⇒ Unbalanced (restoring)force =F=−kx
⇒−mω2x=−kx
⇒ω=√kM=T.
Topper's Solved these Questions
Similar Questions
Knowledge Check
- Question 1 - Select One
An object suspended from a spring exhibits oscillations of period T. Now the spring is cut in two halves and the same object is suspended with two halves as shown in figure. The new time period of oscillation will become
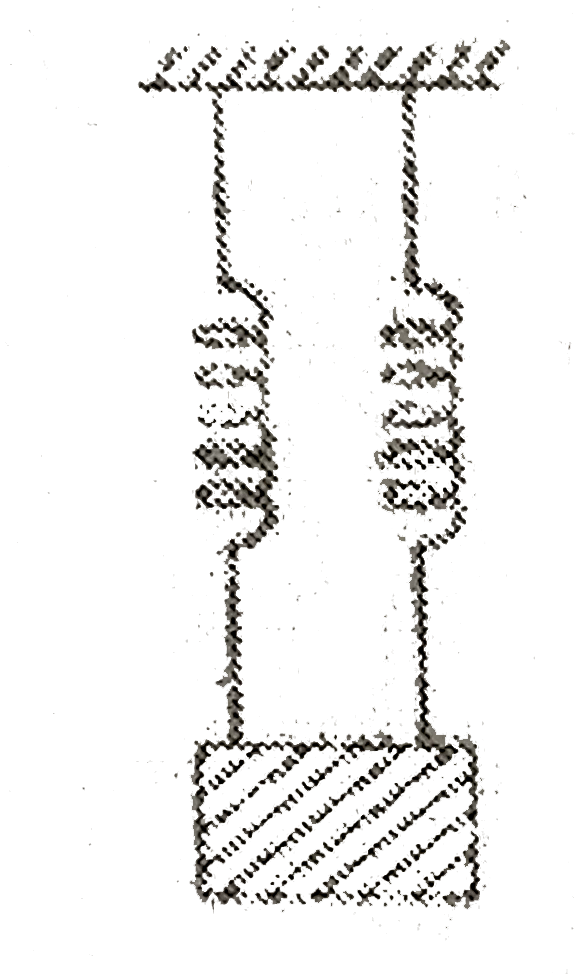 AT√2B2TCT2DT2√2
AT√2B2TCT2DT2√2 - Question 2 - Select One
An object suspended from a spring exhibits oscillations of period T. Now the spring is cut in two halves and the same object is suspsended with two halves as shown in figure. The new time period of oscillation will become
 AT√2B2TCT2DT2√2
AT√2B2TCT2DT2√2 - Question 3 - Select One
A block of mass ma is suspended vertically with a spring of spring constant k. The block is made to oscillate in a gravitation field. Its time period is found to be T. Now the space between the plates is made gravity free, and an electric field E is produced in the downward direction. Now the block is given a charge q. the new time period of oscillation is
 ATBT+2π√qEmdC2π√qEmdDnone of the above
ATBT+2π√qEmdC2π√qEmdDnone of the above
When a mass M is suspended from a spring, its period of oscillation is 2 second. If a mass 4 M is suspended from the same spring, then its period of oscillation will be
View SolutionT1,T2 are time periods of oscillation of a block when individually suspended to springs of force constants K1,K2 respectively. If same block is suspended to series combination of same two springs, then it time period of oscillation.
View SolutionIn a spring block system if length of the spring is reduced by 1%, then time period
View SolutionA block of mass m compresses a spring iof stifffness k through a distacne l/2 as shown in the figure .If the block is not fixed to the spring the period of motion of the block is
 View Solution
View SolutionIn the figure, the block of mass m, attached to the spring of stiffness k is in correct with the completely elastic wall, and the compression in the spring is e. The spring is compressed further by e by displacing the block towards left and is then released. If the collision between the block and the wall is completely eleastic then the time period of oscillation of the block will be
 View Solution
View Solution



