A prism shaped styrofoam of density ρstyrofoam(<ρwater) is held completely submerged in water. It lies with its base horizontal. The base of foam is at depth h0 below water surface and atmospheric pressure is P0 Surface of water is open to atmosphere. Styrofoam prism is held in equilibrium by the string attached symmetrically as shown (Take ρstyrofoam=ρf,ρwater=ρw).
Magnitude of force on any one of the slant face of styrofoam is
(P0+ρg(h0−√2l)Ll
(P0+ρg(h0−l√2))Ll
(P0−ρg(h0−l√2))Ll
(P0+ρg(h0−l2√2))Ll
NA
Topper's Solved these Questions
Similar Questions
A small air bubble of radius r in water is at depth h below the water surface. If P0 is the atmospheric pressure, ρ is the density of water and T is the surface tension of water, what is the pressure inside the bubble?
View SolutionA small air bubble of radius 'r' is at a depth 'h' below the water surface (density of water=ρ). Surface tension of water is T, atmospheric pressure is p0. Find pressure inside the air bubble for the condition r<<h
View Solution
Knowledge Check
- Question 1 - Select One
A prism shaped styrofoam of density ρstyrofoam(<ρwater) is held completely submerged in water. It lies with its base horizontal. The base of foam is at depth h0 below water surface and atmospheric pressure is P0 Surface of water is open to atmosphere. Styrofoam prism is held in equilibrium by the string attached symmetrically as shown (Take ρstyrofoam=ρf,ρwater=ρw).
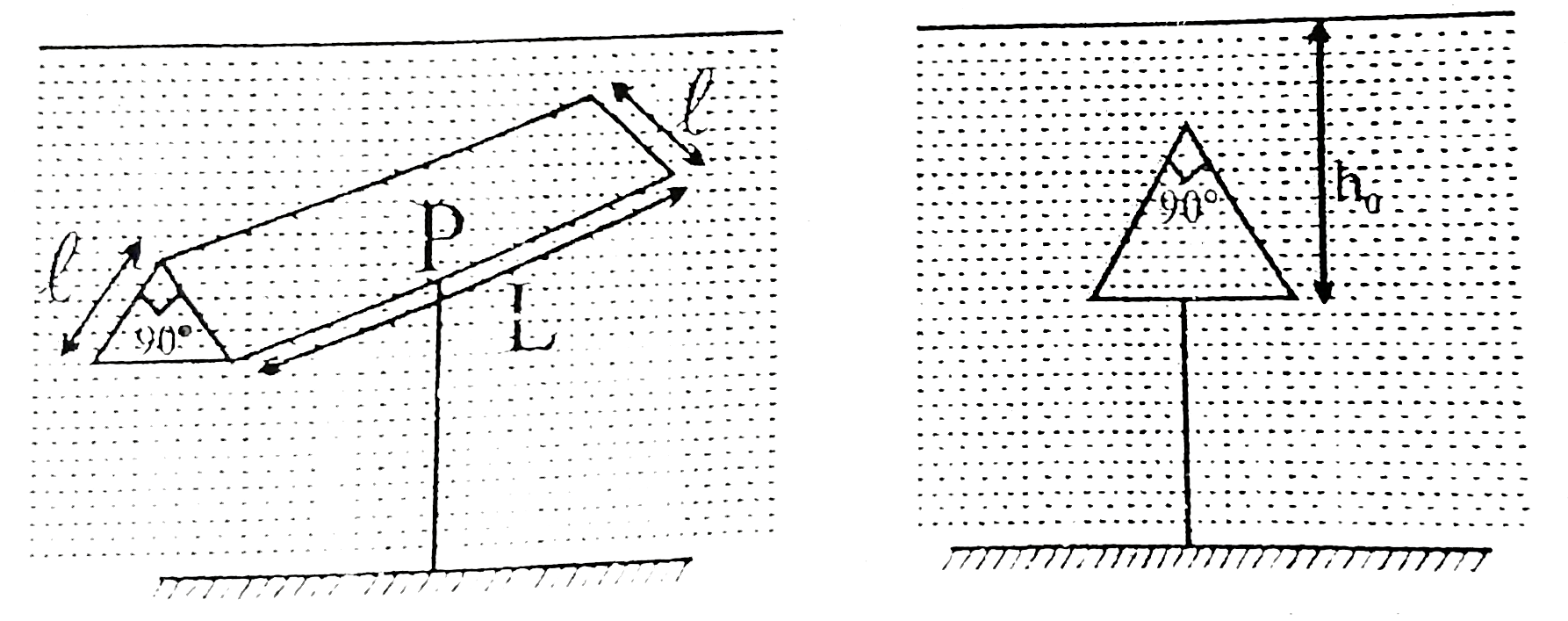Net force exerted by liquid on the styrofoam is A√2ρwgl2LB2ρwgl2LCρwg(l2L)2Dρwgl2L - Question 2 - Select One or More
A prism shaped styrofoam of density ρstyrofoam(<ρwater) is held completely submerged in water. It lies with its base horizontal. The base of foam is at depth h0 below water surface and atmospheric pressure is P0 Surface of water is open to atmosphere. Styrofoam prism is held in equilibrium by the string attached symmetrically as shown (Take ρstyrofoam=ρf,ρwater=ρw).
Now string is cut and styrofoam is allowed to come to surface. A point mass is to be placed symmetrically on the upper surface of styrofoam such that it is in equilibrium with its base in horizontal plane. In equilibrium position styrofoam has half of its slant length submerged. Surface tension of water is T. contact angle is 0^(@). Determine mass m to achieve equilibrium.
AρfgLl22+34ρwgLl2−2T[L+l]B−ρfgLl22+38ρwgLl2−√2T[L+l]C−ρfgLl22+38ρwgLl2−T[L+l)√2DNone of these - Question 3 - Select One
The pressure at depth h below the surface of a liquid of density ρ open to the atmosphere is
Agreater than the atmospheric pressure by ρghBless than the atmospheric pressure by ρghCequal to the atmospheric pressureDincreases exponentially with depth
The absolute pressure at a depth h below the surface of a liquid of density ρ is [Given Pa = atmospheric pressure, g = acceleration due to gravity]
View SolutionThe density of water at the surface of ocean is ρ . If the bulk modulus of water is B, then the density of ocean water at depth, when the pressure is αp0 and p0 is the atmospheric pressure is
View SolutionIf the atompspheric pressure is Pa then the jpressure P at depth a below the surface of a liquid of density ρ open to the atmosphere is
View SolutionThe radius of the biggest metal coin of thickness t and density ρ which would be able to float on water surface of surface of water is ρ
View SolutionWhen unit mass of water boils to become steam at 100∘C, it absorbs Q amount of heat. The densities of water and steam at 100∘C are ρ1 and ρ2 respectively and the atmospheric pressure is P0. The increase in internal energy of the water is
View Solution