An open pan P filled with water of density (ρw) is placed on a vertical rod, maintaining equilibrium. A block of density ρ is placed on one side of the pan as shown. Water depth is more then height of the block.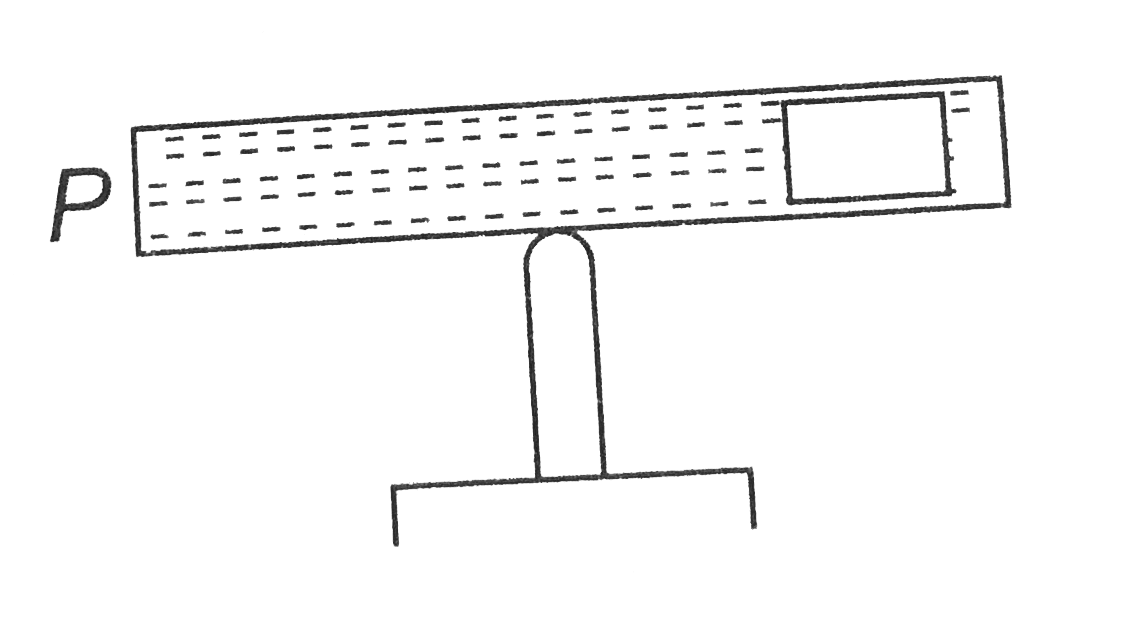 
Equilibrium will be maintainer only if ρ<ρW.
Equilibrium will be maintainer only if ρ≤ρW.
Equilibrium will be maintainer for all realtlion between ρ and ρw.
It is not possible to maintained the equilibrium
The correct Answer is:B
Step by step video, text & image solution for An open pan P filled with water of density (rho_w) is placed on a vertical rod, maintaining equilibrium. A block of density rho is placed on one side of the pan as shown. Water depth is more then height of the block. by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Topper's Solved these Questions
- BOOK - RESONANCECHAPTER - FLUID MECHANICSEXERCISE - Exercise- 2 PART - II9videos
FLUID MECHANICS
- BOOK - RESONANCECHAPTER - FLUID MECHANICSEXERCISE - Exercise- 2 PART - III8videos
FLUID MECHANICS
- BOOK - RESONANCECHAPTER - FLUID MECHANICSEXERCISE - Exercise- 1 PART - II Section (C)6videos
FLUID MECHANICS
- BOOK - RESONANCECHAPTER - ELECTROSTATICSEXERCISE - Exercise52videos
ELECTROSTATICS
- BOOK - RESONANCECHAPTER - FULL TEST 1EXERCISE - Exercise30videos
FULL TEST 1
Similar Questions
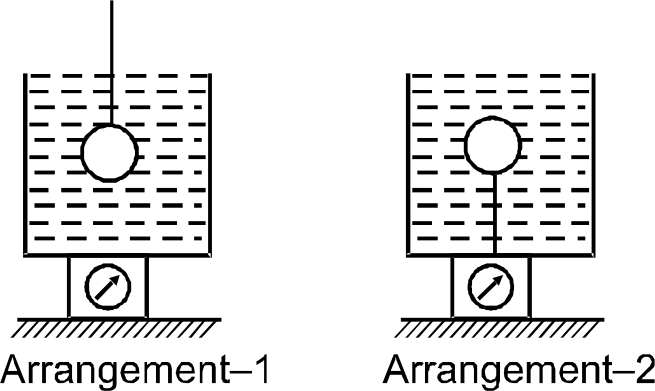
A container open from top, filled with water (density ρw) upto the top, is placed on a weighing machine and the reading is W. A wooden ball of volume V and mass m is put in the water by the given two arrangements. In arrangement–1, the ball is connected by a rigid rod (of negligible volume) and pushed in the water. In arrange- ment–2, the ball is attached with bottom by a massless string. The reading of weighing machine, (density of wood is less than water) (choose incorrect option)
View SolutionA cylindrical block of the density ρ is partically immersed in a liwuid of density 3ρ. The plane surface of the block remains parallel to the surface of the liquid. The height of the block is 60m. The block perform SHM when displaced form its mean position [Use g=9.8m/s2]
View Solution
Knowledge Check
- Question 1 - Select One
An open pan P filled with water (density ρm) is placed on one side of the pan as shown. If water depth is more then height of the block, then choose the correct statement.
AEquilibrium will be maintained only if ρ<ρw.BEquilibrium will be maintained only ρ≤ρw.CEquilibrium will be maintained for all relation between ρandρw.DEquilibrium will not be maintained in all cases. - Question 2 - Select One
A block of density ρ floats in a liquid with its one third volume immersed. The density of the liquid is
AρBρ3Cρ2D3ρ - Question 3 - Select One
Cylindrical block of area of cross-section A and of material of density ρ is placed in a liquid of density one third of density of block. The block compress in the spring is one-third of te length of the block. if acceleration due to gravity is g, the spring constant of the spring isAρAgB2ρAgC2ρAg/3DρAg/3
A uniform rod of density ρ is placed in a wide tank containing a liquid of density ρ0(ρ0>ρ). The depth of liquid in the tank is half the length of the rod. The rod is in equilibrium, with its lower end resting on the bottom of the tank. In this position the rod makes an angle θ with the horizontal.
View SolutionA cylindrical tank has a hole of diameter 2r in its bottom. The hole is covered wooden cylindrical block of diameter 4r, height h and density ρ/3.
Situation I: Initially, the tank is filled with water of density ρ to a height such that the height of water above the top of the block is h1 (measured from the top of the block).
Situation II: The water is removed from the tank to a height h2 (measured from the bottom of the block), as shown in the figure. The height h2 is smaller than h (height of the block) and thus the block is exposed to the atmosphere.
Find the minimum value of height h1 (in situation 1), for which the block just starts to move up?View SolutionA cylindrical tank has a hole of diameter 2r in its bottom. The hole is covered wooden cylindrical block of diameter 4r, height h and density ρ/3.
Situation I: Initially, the tank is filled with water of density ρ to a height such that the height of water above the top of the block is h1 (measured from the top of the block).
Situation II: The water is removed from the tank to a height h2 (measured from the bottom of the block), as shown in the figure. The height h2 is smaller than h (height of the block) and thus the block is exposed to the atmosphere.
In situation 2, if h2 is further decreased, thenView SolutionThe lower end of a capillary tube of radius r is placed vertically in water of density ρ , surface tension S. The rice of water in the capillary tube is upto height h, then heat evolved is
View SolutionA cylindrical tank has a hole of diameter 2r in its bottom. The hole is covered wooden cylindrical block of diameter 4r, height h and density ρ/3.
Situation I: Initially, the tank is filled with water of density ρ to a height such that the height of water above the top of the block is h1 (measured from the top of the block).
Situation II: The water is removed from the tank to a height h2 (measured from the bottom of the block), as shown in the figure. The height h2 is smaller than h (height of the block) and thus the block is exposed to the atmosphere.
Find the height of the water level h2 (in situation 2), for which the block remains in its origin) position whithout the application of any external forceView Solution