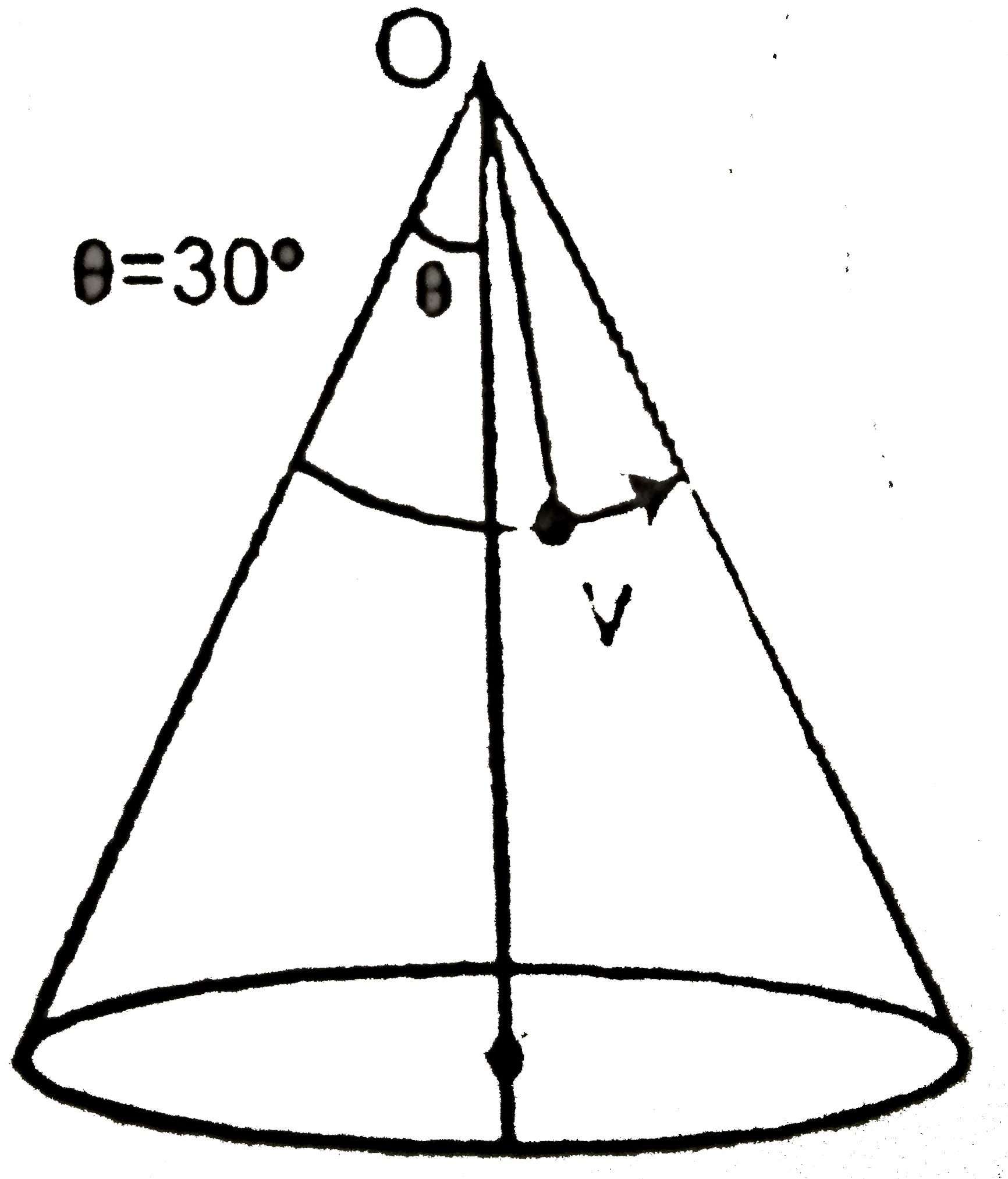
Three masses of small size are attached by light inextensible strings of various lengths to a point O on the ceiling. All of the masses swing round in horizontal circles of various radii with the same angular frequency ω (one such circle is drawn in the shown figure.) Then pick up the correct statement.
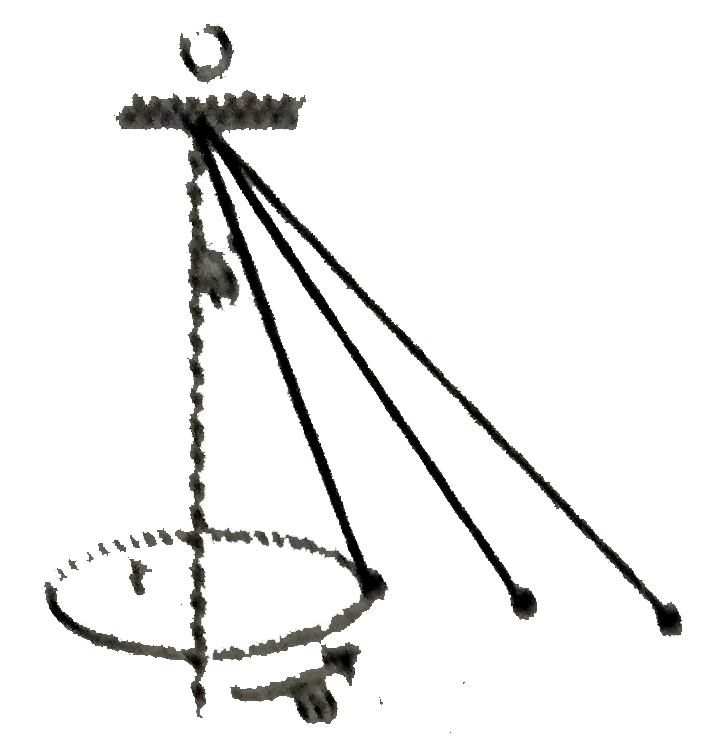
The vertical depth of each mass below point of suspension from ceilling is different
the radius of horizontal circular path of eachmass is same
all masses revolve in the same horizontal plane
all the particles must have same mass.
The correct Answer is:C
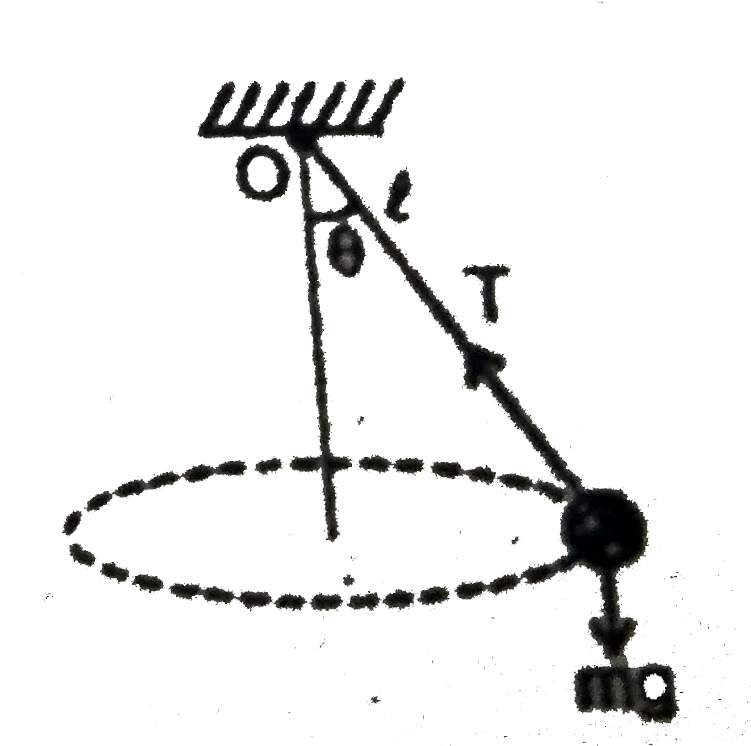
For conical pendulum l , mass m moving
along horizontal circle is as shown
Tcosθ=mg.....(1)
Tsinθ=mω2lsinθ.....(2)
From equation (1) and equation (2), lcosθ=gω2
lcosθ is the vertical distance of below O point of suspension. hence if ω of all three pendulum are same, they small revolve in same horizontal plane.
Alternate.
If we remember that time period T of conical pendulum is
T=2π√Lg where L is the vertical path of bob below point of suspension. If T is same for three pendulum
even L shall be also same. hence all three particles shall revolve in same horizontal plane
Topper's Solved these Questions
Similar Questions
Three balls each of mass 1 kg are attached with three strings each of length 1 m as shown in figure. They are rotated in a horizontal circle with angular velocity ω=4rad s−1 about point O. Match the following columns.
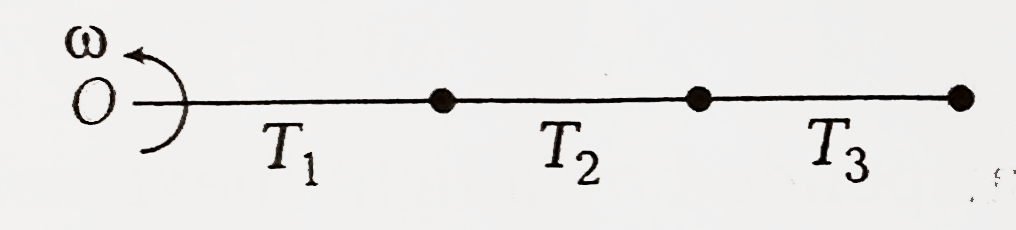
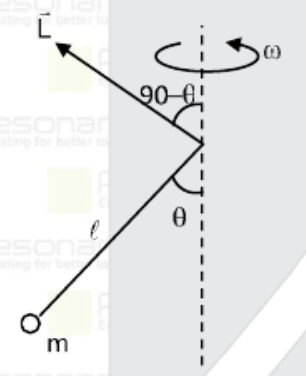
View SolutionA bob of mass m attached to an inextensible string of length l, is suspended from a vertical support. Bob rotates in a horizontal circle with angular speed ω and string makes an angle of θ with the vertical. Find the angular momentum of bob about axis of rotation
View Solution
Knowledge Check
Three point masses are attached by light inextensible strings of various lengths to a point O on the ceiling. All of the masses swing round in horizontal circles of various radii with the same angular frequency ω (one such circle is drawn in the shown figure.) Then pick up the correct statement.
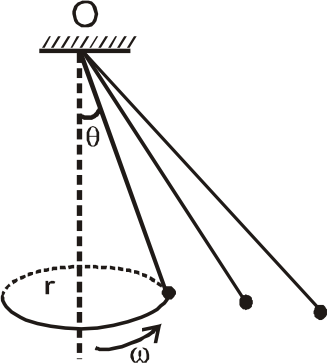 AThe vertical depth of each mass below point of suspension from ceilling is different.BThe raduis of horizontal circular path of each mass is same.CAll masses revolve in the same horizontal plane.DAll the particles must have same mass.
AThe vertical depth of each mass below point of suspension from ceilling is different.BThe raduis of horizontal circular path of each mass is same.CAll masses revolve in the same horizontal plane.DAll the particles must have same mass.A uniform chain of mass M and length L is rotated in a horizontal circle about its one end at an angular frequency ω. The tension at its axis is
AMω2LBMω2L8CMω2L4DMω2L2A bob of mass m attached to an inextensible string of length I is suspended from a vertical support. The bob rotates in a horizontal circle with an angular speed ω red/s about the vertical. About the point of suspension:
Aangular momentum is conserved.Bangular momentum changes in magnitude but not is direction.Cangular momentum changes in direction but not in magnitude.Dangular momentum changes both in direction and magnitude.
A small ball of mass 100g is attached to a light and inextensible string of length 50cm. The string is tied to a support O and the mass m released from point A which is a' a horizontal distance of 30cm from the support. Calculate the speed of the ball is its lowest point of the trajectory.
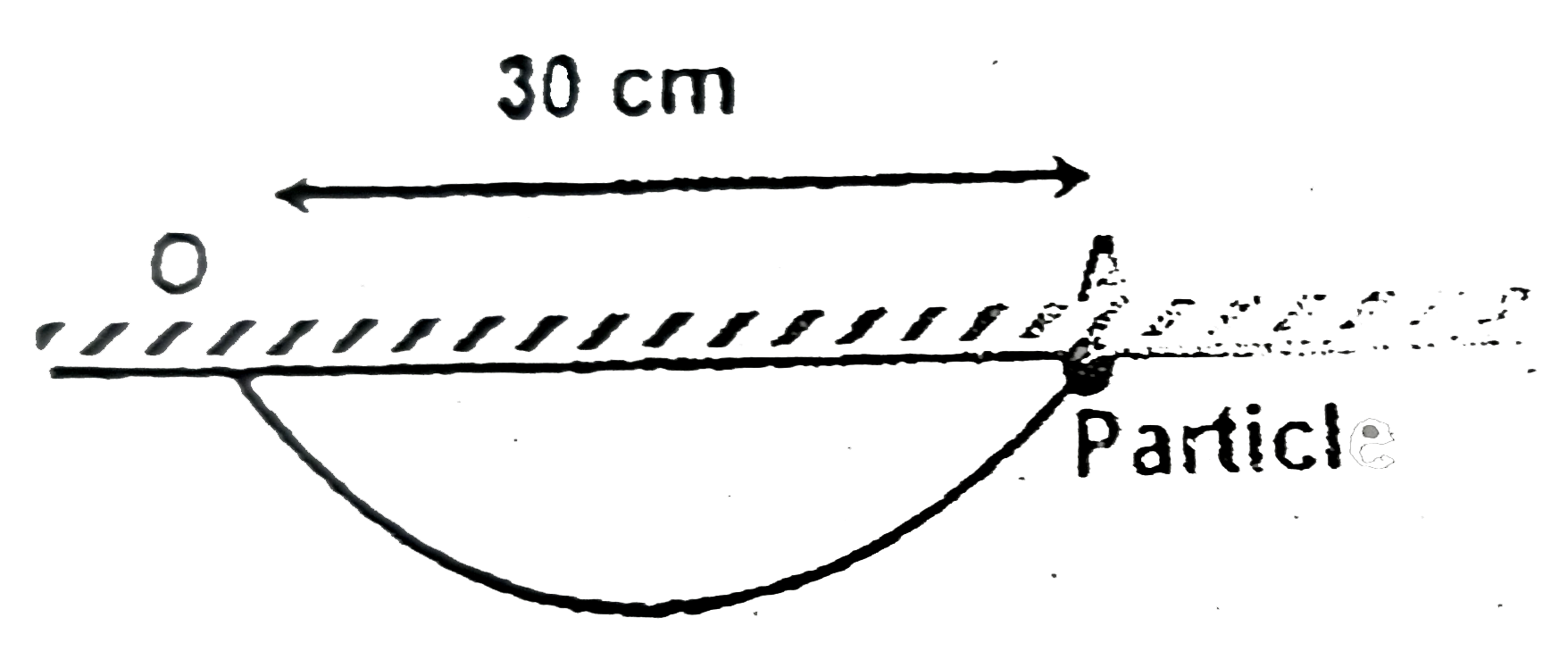
View SolutionA small ball of mass m suspended from the celling at a point O by a thread of length l moves along a horizontal circle with a constant angular velocity ω.
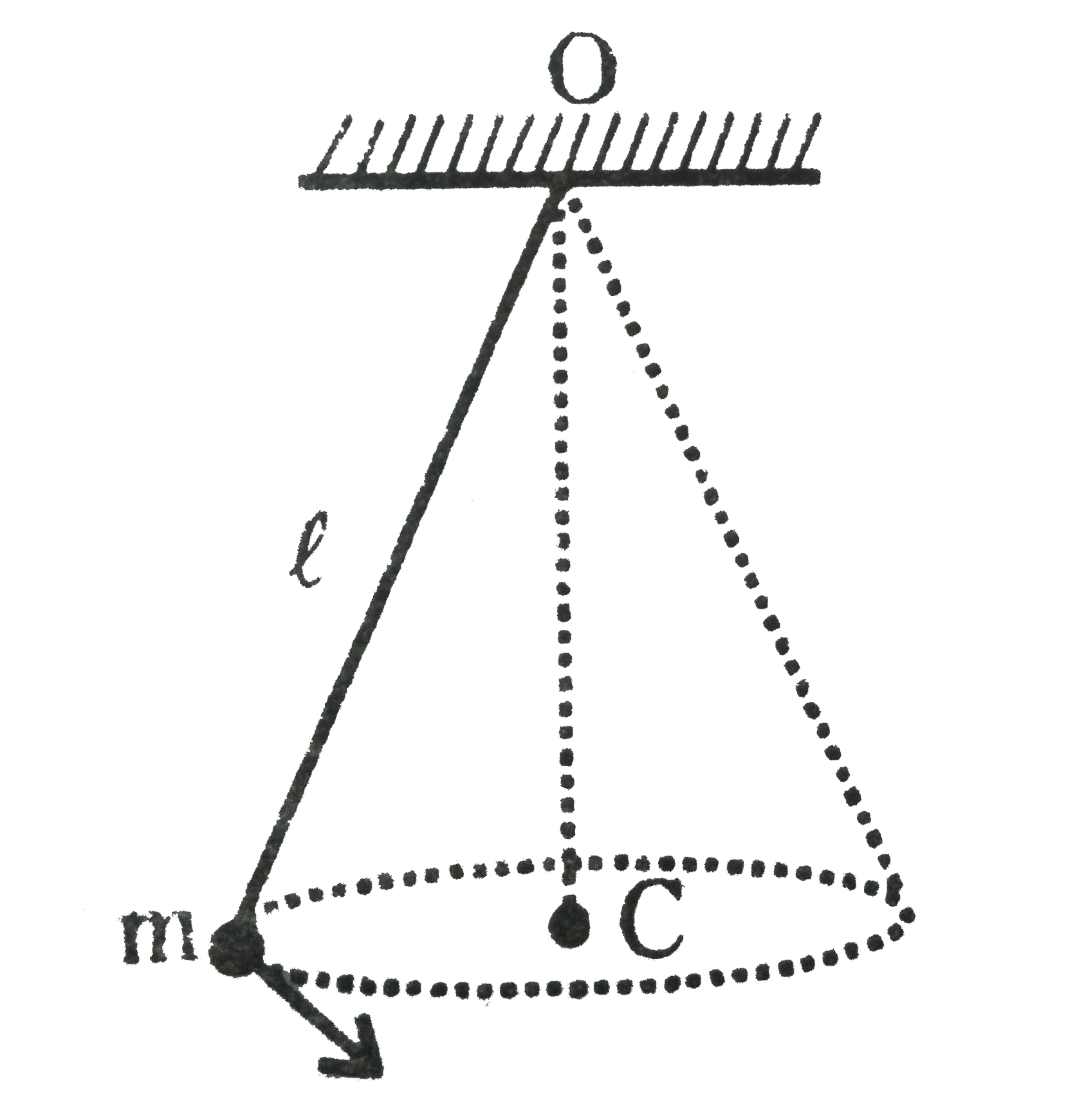 .
.
View Solution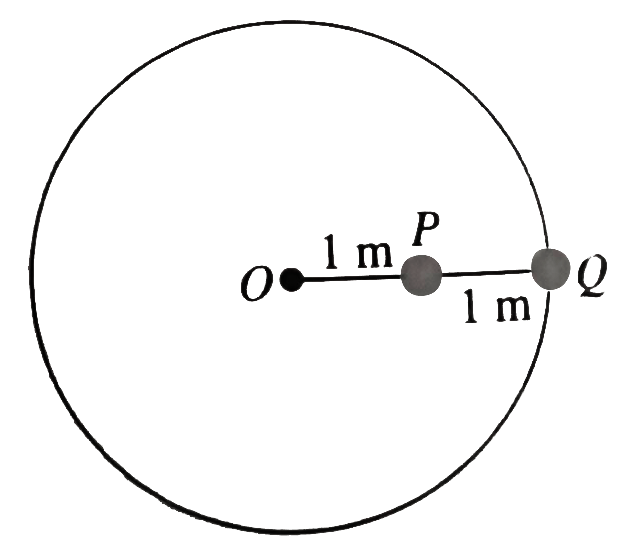
Two spheres of equal masses are attached to a string of length 2 m as shown in figure. The string and the spheres are then whirled in a horizontal circle about O at a constant rate. What is the value of the ratio:
View SolutionA particle is attached by a light string of length 3 a to a fixed point and describes a horizontal circle of radius a with uniform angular velocity ω If, when the particle is moving in this manner, is suddenly stopped and then let go,find its velocity when the string is vertical in its subsequent motion :
View SolutionA bob of mass 2kg is suspended from point O of a core with an inextensible string strinng of length √3m. It is moving in horizontal circle over the surface of cone as shown in the figure. Then :(g=10m/s2)
View Solution
