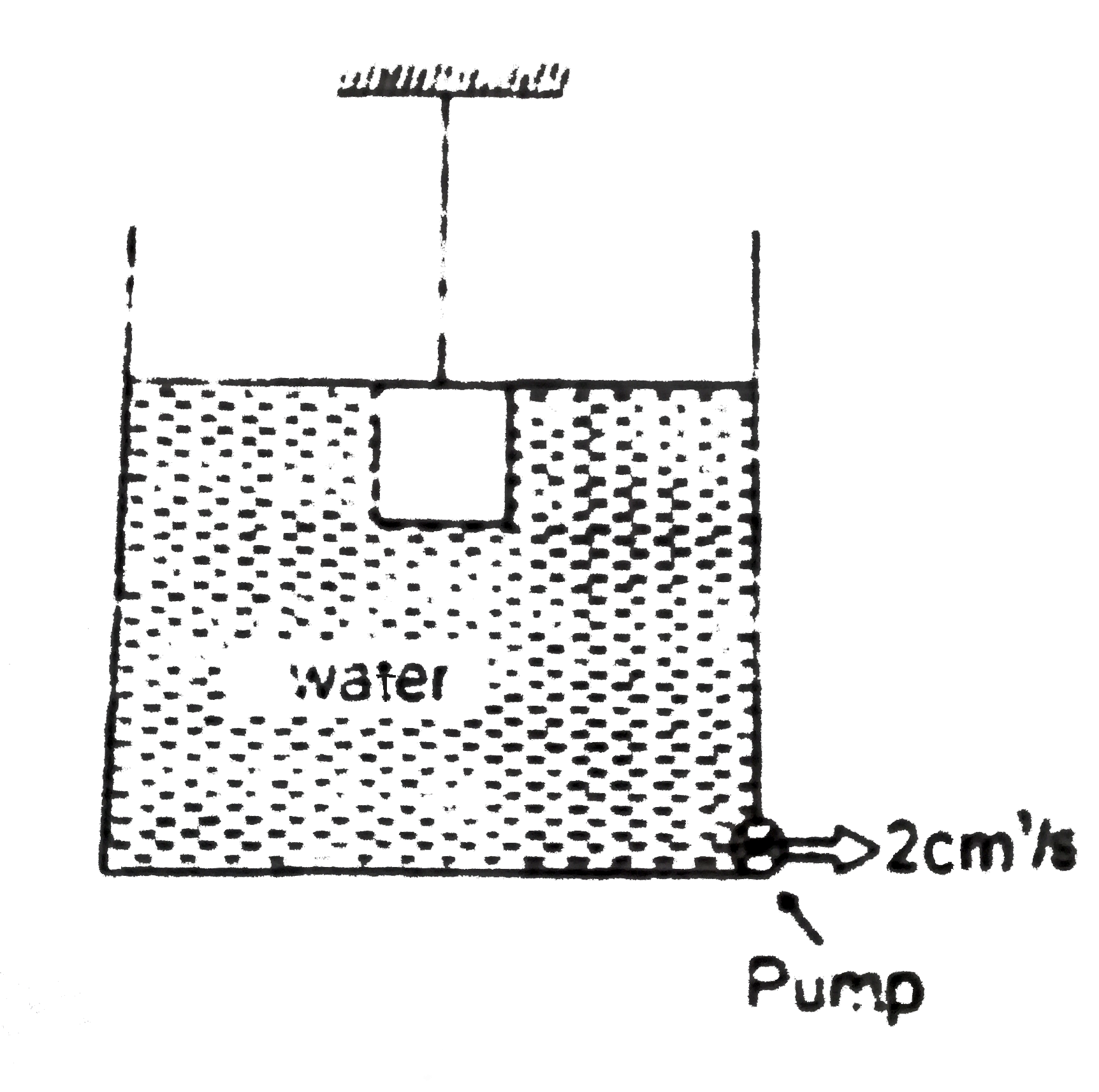
Figure shows a cubical block of side 10 cm and relative density 1.5 suspended by a wire of cross sectional area 10−6m2. The breaking stress of the wire is 7×106N/m2. The block is placed in a beaker of base area 200cm2 and initially i.e. at t = 0, the top surface of water & the block coincide. There is a pump at the bottom corner which ejects 2cm3 of water per sec. Find the time at which the wire will break.
The correct Answer is:5
Breaking force = Breaking stress × area of wire
=7×106×10−6=7N
weight of block =vol×density×g
10−3×(1.5×103)×10
=15N.
The upthrust when the liquid level has decended by xcm.
=100(10−x).10−6.103.10
=10−x Newton.
∴ Net downward force on the block =15−(10−x)=5+x=TansionT
∴ The wire will break when 5+x=7.
i.e. when x=2cm
Let the level decends by 2cm in t time
then 2t=(200−100).2
t=100sec. ........Ans.
20x=10∴x=5
Topper's Solved these Questions
- BOOK - RESONANCECHAPTER - FLUID MECHANICSEXERCISE - Exercise- 2 PART - III8videos
FLUID MECHANICS
- BOOK - RESONANCECHAPTER - FLUID MECHANICSEXERCISE - Exercise- 2 PART - IV10videos
FLUID MECHANICS
- BOOK - RESONANCECHAPTER - FLUID MECHANICSEXERCISE - Exercise- 2 PART - I18videos
FLUID MECHANICS
- BOOK - RESONANCECHAPTER - ELECTROSTATICSEXERCISE - Exercise52videos
ELECTROSTATICS
- BOOK - RESONANCECHAPTER - FULL TEST 1EXERCISE - Exercise30videos
FULL TEST 1
Similar Questions
Knowledge Check
- Question 1 - Select One
A resistance of 50Ω is to be prepared using a wire of cross-sectional area 10−8m2 and conductivity 2.2×106 siemens/metre. The length of the wire required is
A22.5 mB11 mC1.1 mD2.2 m. - Question 2 - Select One
A body of mass 500 g is fastened to one end of a steel wire of length 2m and area of cross-section 2mm2. If the breaking stress of the wire is 1.25×107N/m2, then the maximum angular velocity with which the body can be rotated in a horizontal circle is
A2 rad/sB3 rad/sC4 rad/sD5 rad/s - Question 3 - Select One
A current of 0.01 A flows through a potentiometer wire of cross section area 10−6m2. If the specific resistance of the potentiometer wire is 10−7 ohm-m, then the potential gradient will be
A10−1V/mB10−3V/mC10−2V/mD0.5×10−2V/m
The current in a metal wire of cross-sectional area 10−6m2 is 1.6A .If the free electron density of the metal is 8×1028m−3 then the drift speed of electrons is
View SolutionA 4.0 m long copper wire of cross sectional area 1.2cm2 is stretched by a force of 4.8×103 N stress will be -
View SolutionCalculate the force required to increase the length of a steel wire of cross- sectional area 10−6m2 by 0.5% given: Y(for steel)=2×1011N−m2
View SolutionA wire of length 1m is stretched by a force of 10N. The area of cross-section of the wire is 2×10–6m2 and Y is 2×1011N/m2 . Increase in length of the wire will be -
View SolutionA current of 5A is passing through a metallic wire of cross-section area 4×10−6m2. If the density of the charge carries in the wire is 5×1036/m3, the drift velocity of the electrons is.
View Solution

