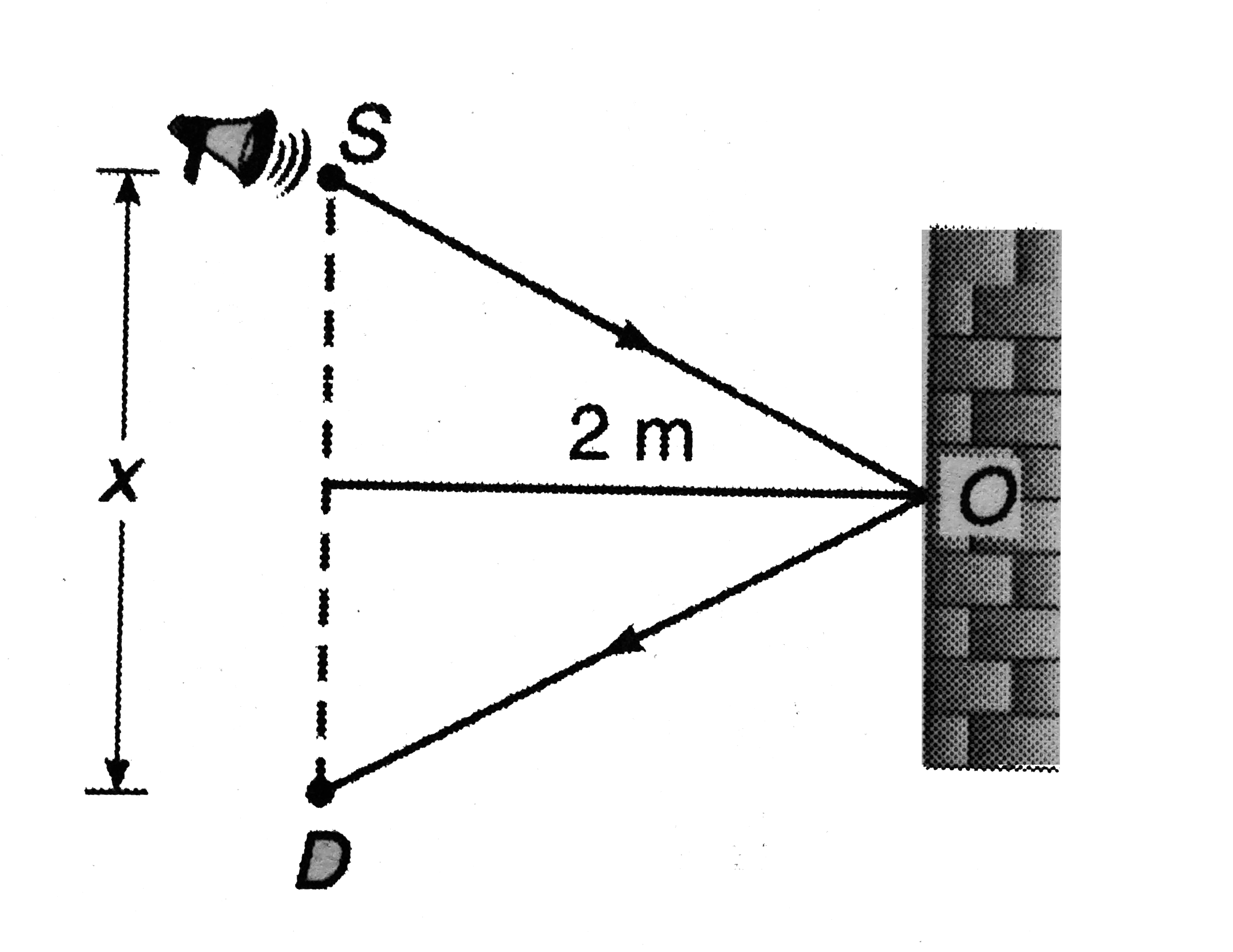
A source emitting sound of frequency $165 H z$ is placed in frount of a wall at a distance of $2 m$ from it. A detector is also placed in fornt of the wall at the same distance from it. Find the distance between the source and the detector for which the detector detects phase difference of $2 π$ between the direct and reflected wave. Speed of sound in air $= 330 m / s$ .

Video Solution

Text Solution

Verified by Experts

The situation is shown in figure. Suppose the detector is placed at a distance of $x$ meter from the source. The direct wave received from the source travels a distance of $x$ meter. The wave reaching the detector after reflection from the wall has travelled a distance of $2 {[{(2)}^{2} + x^{2} / 4]}^{1 / 2}$ meter. The path difference between the two waves is
$Δ = {2 {[{(2)}^{2} + \frac{x^{2}}{4}]}^{1 / 2} - x} m e t e r$ .
$Δ = λ$ for $Δ ϕ = 2 π ... (i)$
Thus, by $(i) 2 {[{(12)}^{2} + \frac{x^{2}}{4}]}^{1 / 2} - x = 2$
or, $[4 \times \frac{x^{2}}{2}]$ or, $4 + \frac{x^{2}}{4} = 1 + \frac{x^{2}}{4} + x$
or, $x = 3$
Thus, the dector should be placed at a distance of $3 m$ from the source, Note that there is no abrupt phase change.

Updated on:21/07/2023

A source emitting sound of frequency $180 H z$ is placed in front of a wall at distance of $2 m$ from it . A detector is also placed in front of the wall at the same distance from it. Find the minimum distance between the source and the detector for which the detector detects a maximum of sound. Speed of sound in air $= 360 m / s$ .
A $3 m$
B $2 m$
C $3 / 2 m$
Dzero
A soure of sound of frequency 165 hz is placed in front of a wall at a distance 2 m from it. A dtector is also placed in front of the wall at the same distance from it. Find the minimum distance between the source and detector for which maximum sound is recorded int he detector . the speed of sound is 330 m/s
A4m
B3 m
C1 m
D2m
When a sound wave is reflected from a wall the phase difference between the reflected and incident pressure wave is:
A $0$
B $p$
C $p / 2$
D $p / 4$