A string $25 c m$ long fixed at both endds and having a mass of $2.5 g$ is under tension. A pipe closed from one end is $40 c m$ long. When the strin is set vibrating in its first overtone and the air in the pipe in its fundamental frequency, $8$ beats per second are heard. If is observed that decreasing the tension in the string decreases the beat frequency. If the speed of sound in air is $320 m / s$ . Find tension in the string.

Video Solution

Text Solution

Verified by Experts

$μ = \frac{2.5}{25} = 0.1 g / c m = 10^{- 2} K g / m$
$1^{s t}$ overtone

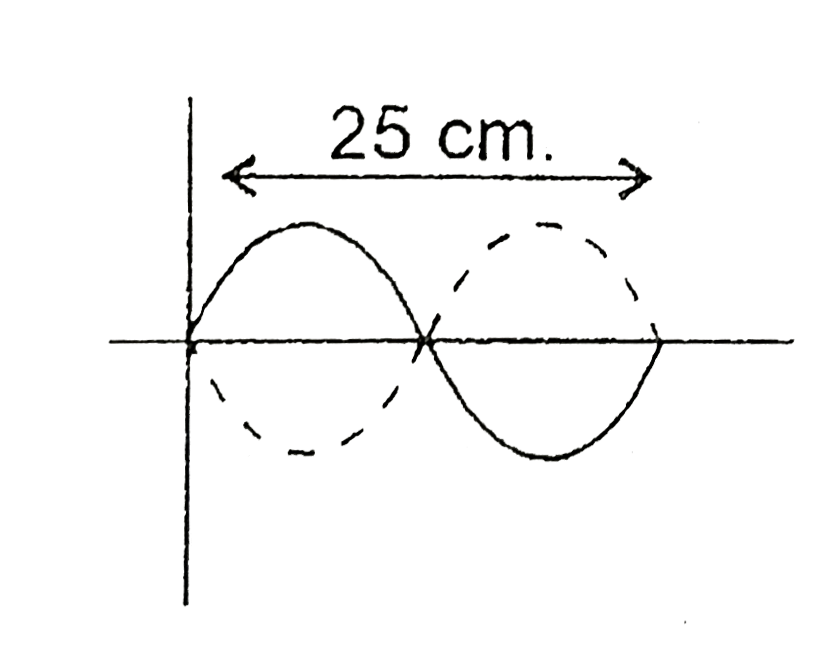
$λ_{s} = 25 c m = 0.25 m \Rightarrow f_{s} = \frac{1}{λ_{s}} \sqrt{\frac{T}{μ}}$
pipe is fundamental freq
$λ_{p} = 160 c m = 1.6 m \Rightarrow f_{p} = \frac{V}{λ_{p}}$

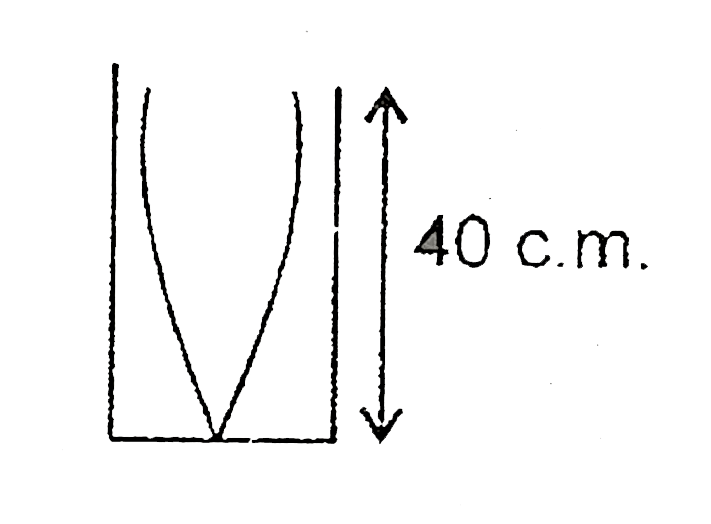
$∵$ by decreasing the tension, beat freq is decreased
$∴ f_{s} < f_{p} \Rightarrow f_{s} - f_{p} = 8 \Rightarrow \frac{1}{0.25} \sqrt{\frac{T}{10^{- 2}}} - \frac{320}{1.6} = 8 \Rightarrow T = 27.04 N$

Updated on:21/07/2023

A string of length $50 c m$ and mass $12.5 g$ is fixed at both ends. A pipe closed at one end has a length $85 c m$ . When the string vibrates in its second overtone and the air column in the pipe in its first. Overtone, they produce a beats frquency of $6 H z$ . It is also observed that decreasing teh tension in the string decreaes beats frequency. Neglect the end correction in the pipe and velocity of sound in air is $340 m / s$ . then the tension in the string is
A $72 N$
B $52 N$
C $26 N$
D $18 N$
A tuning fork of frequency 512 Hz is vibrated with sonometer wire and 6 beats per seconds are heard. The beat frequency reduces if the tension in the string is slightly increased. The original freqency of vibration of the string is
A506 Hz
B512 Hz
C518 Hz
D524 Hz
A stretched string of length $1 m$ fixed at both ends , having a mass of $5 \times 10^{- 4} k g$ is under a tension of $20 N$ . It is plucked at a point situated at $25 c m$ from one end . The stretched string would vibrate with a frequency of
A $400 H z$
B $100 H z$
C $200 H z$
D $256 H z$