The centre of mass of the shaded portion of the disc is: ( The mass is uniformly distributed in the shaded portion).
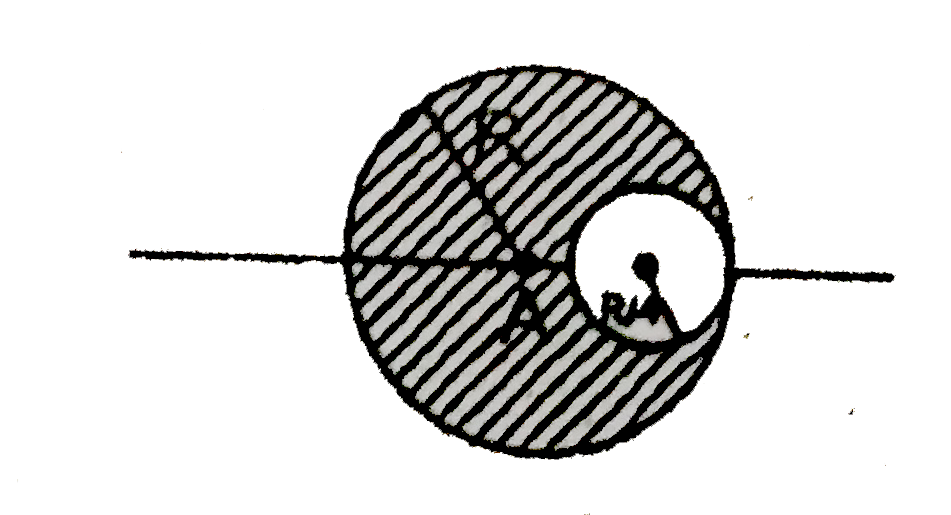
R20 to the left of A
R12 to the left of A
R20 to the right of A
R12 to the right of A
The correct Answer is:A
Step by step video & image solution for The centre of mass of the shaded portion of the disc is: ( The mass is uniformly distributed in the shaded portion). by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- SYSTEM OF PARTICLES AND ROTATIONAL MOTIONBOOK - VMC MODULES ENGLISHCHAPTER - SYSTEM OF PARTICLES AND ROTATIONAL MOTIONEXERCISE - EFFICIENT
50 Videos
- SYSTEM OF PARTICLES AND ROTATIONAL MOTIONBOOK - VMC MODULES ENGLISHCHAPTER - SYSTEM OF PARTICLES AND ROTATIONAL MOTIONEXERCISE - IMPECCABLE
56 Videos
- SYSTEM OF PARTICLES AND ROTATIONAL MOTIONBOOK - VMC MODULES ENGLISHCHAPTER - SYSTEM OF PARTICLES AND ROTATIONAL MOTIONEXERCISE - IMPECCABLE
56 Videos
- SYSTEM OF A PARTICLES & ROTATIONAL MOTIONBOOK - VMC MODULES ENGLISHCHAPTER - SYSTEM OF A PARTICLES & ROTATIONAL MOTIONEXERCISE - IN-CHAPTER EXERCISE F
10 Videos
- UNITS, MEASUREMENTS & ERRORSBOOK - VMC MODULES ENGLISHCHAPTER - UNITS, MEASUREMENTS & ERRORSEXERCISE - IN - CHAPTER EXERCISE - B
10 Videos
Similar Questions
The centre of mass of the shaped portion of the disc is (The mass is uniformly distributed in the shaded portion)

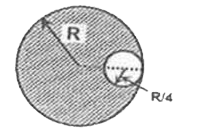
View SolutionFind the centre of mass of the shaded portion of a disc.
View SolutionFind the centre of mass of the section. Consider the mass of the lamina to be uniformly distributed.

View SolutionWrite the fraction of the shaded portion in the following figures.
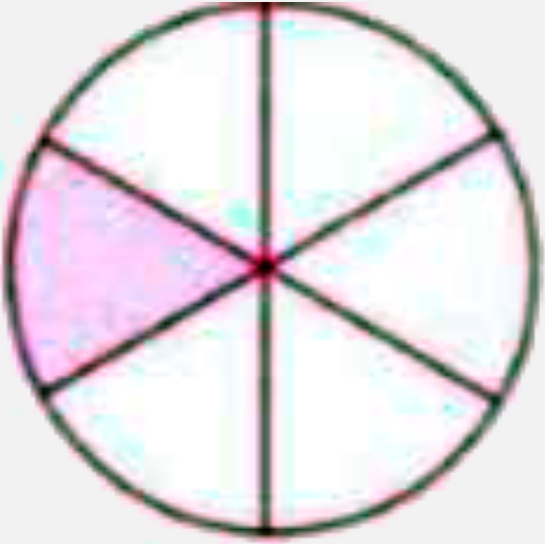
View SolutionWrite the fraction of the shaded portion in the following figures.
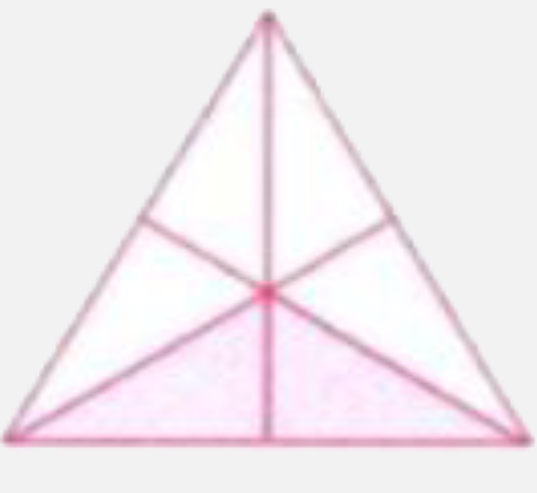
View SolutionWrite the fraction of the shaded portion in the following figures.

View SolutionWrite the fraction of the shaded portion in the following figures.
View SolutionWrite the fraction of the shaded portion in the following figures.

View SolutionWrite the fraction of the shaded portion in the following figures.
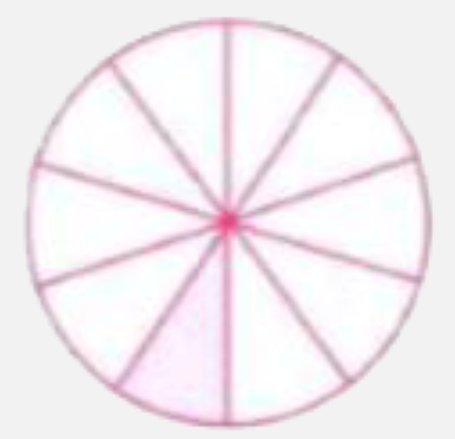
View SolutionA uniform circular disc of mass M and radius R is pivoted at distance x above the centre of mass of the disc, such that the time period of the disc in the vertical plane is infinite. What is the distance between the pivoted point and centre of mass of the disc ?
View Solution
