A body of mass $m$ is dropped from a height of $h$ . Simultaneously another body of mass $2 m$ is thrown up vertically with such a velocity $v$ that they collide at height $\frac{h}{2}$ . If the collision is perfectly inelastic, the velocity of combined mass at the time of collision with the ground will be

A

$\sqrt{\frac{5 g h}{4}}$

B

$\sqrt{g h}$

C

$\sqrt{\frac{g h}{4}}$

D

$\frac{\sqrt{10 g h}}{3}$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:D

$v_{2} = \sqrt{2 g (\frac{h}{2})} = \sqrt{g h}$
$t = \sqrt{\frac{2 (\frac{h}{2})}{g}} = \sqrt{\frac{h}{g}}$
Now. using relative motion
$t = \frac{h}{v - 0} \Rightarrow \sqrt{\frac{h}{g}} = \frac{h}{v} \Rightarrow v = \sqrt{g h}$
$v_{1}^{2} = v^{2} - 2 g (\frac{h}{2}) \Rightarrow v_{1}^{2} = g h - g h = 0 \Rightarrow v_{1} = 0$
using conservation of linear momentum
$3 {m v}_{3} = {m v}_{2} - 2 {m v}_{1} \Rightarrow 3 {m v}_{3} = m \sqrt{g h} - 2 m (0) \Rightarrow v_{3} = \frac{1}{3} \sqrt{g h}$
$v_{4}^{2} = v_{3}^{2} + 2 g (\frac{h}{2}) \Rightarrow v_{4}^{2} = \frac{g h}{9} + g h = \frac{10 g h}{9} ∴ v_{4} = \frac{\sqrt{10 g h}}{3}$

|

Updated on:21/07/2023

Class 11 PHYSICS CENTRE OF MASS

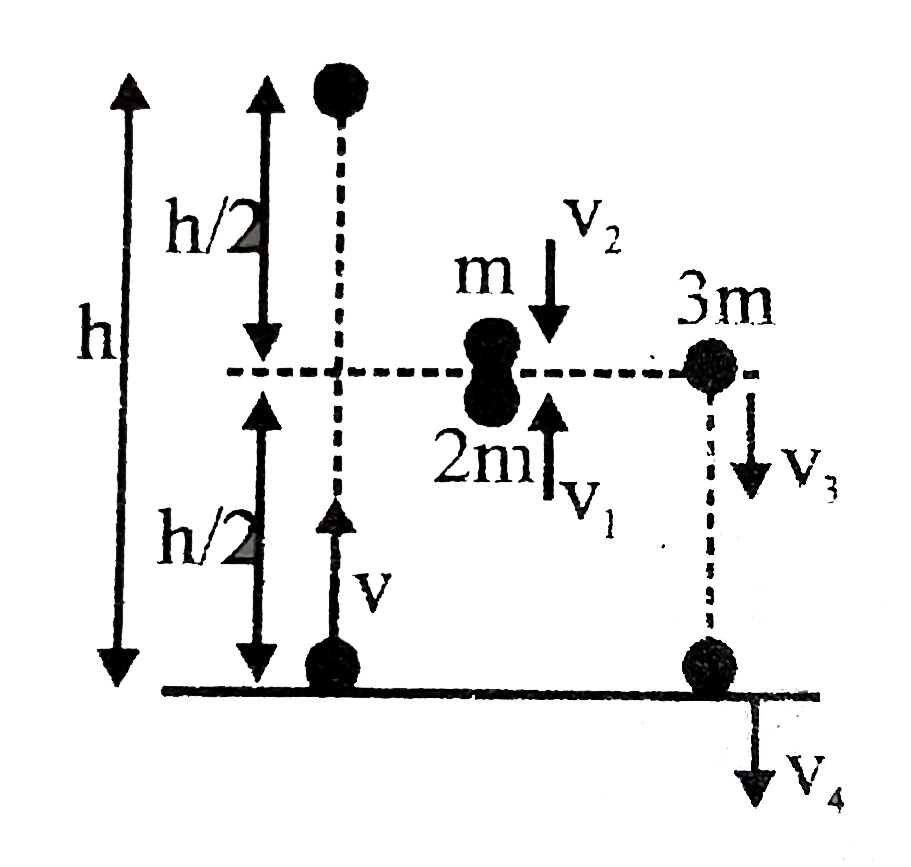
Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
A particle of mass m is dropped from a height h above the ground. Simultaneously another particle of the same mass is thrown vertically upwards from the ground with a speed of $\sqrt{2 g h}$ . If they collide head-on completely inelastically, then the time taken for the combined mass to reach the ground is
A $\sqrt{\frac{3 h}{4 g}}$
B $\sqrt{\frac{3 h}{2 g}}$
C $\sqrt{\frac{h}{2 g}}$
D $\sqrt{\frac{h}{4 g}}$
Question 2 - Select One
A body A of mass 4 kg is dropped from a height of 100 m. Another body B of mass 2 kg is dropped from a height of 50 m at the same time. Then :
ABoth the bodies reach the ground simultaneously.
BA takes nearly ${0.7}^{t h}$ of time required by B
CB takes nearly ${0.7}^{t h}$ of time required by A
DA takes double the time required by B.
Question 3 - Select One
A particle of mass m is dropped from a height h above the ground. At the same time another particle of mass 2m is thrown vertically upwards from the ground with a speed of $\sqrt{g h}$ . If they collide head-on completely inelastically, the time taken for the combined mass to reach the ground, in units of $\sqrt{\frac{h}{g}}$ is:
A $\frac{\sqrt{40} - 2}{6}$
B $\frac{\sqrt{30} - 3}{7}$
C $\frac{\sqrt{20} - 2}{5}$
D $\sqrt{\frac{3}{2}}$

BANSAL-CENTRE OF MASS & MOMENTUM CONSERVATION-EXERCISE-1 [SINGLE CORRECT CHOICE TYPE]

Home
Ask Doubt
Profile