Calculate the quantity of heat conducted through 2m2 of a brick wall 12cm thick in 1hour if the temperature on one side is 8∘C and on the other side is 28∘C. (Thermal conductivity of brick =0.13Wm−1K−1)
Temperature gradient =28−812×10−2Km−1 and t=3600s
∴Q=kAt× temperature gradient
=0.13×2×3600×28−812×10−2
=156000J
Topper's Solved these Questions
Similar Questions
Calculate the rate of loss of heat through a glass window of area 1000cm2 and thickness 0.4 cm when temperature inside is 37∘C and outside is −5∘)C . Coefficient of thermal conductivity of glass is 2.2×10−3cals−1cm−1K−1.
View SolutionA copper slab is 2 mm thick. It is protected by a 2 mm layer of stainless steel on both sides. The temperature on one side of this composite slab is 400∘C and 200∘C on the other side. Value of thermal conductivities are-
kcu=400Wm−1K−1 and ks=16Wm−1K−1
(a) Just by knowing that thermal conductivity of steel is much less than copper, find (approximately) the temperature of the copper slab.
(b) Plot the variation of temperature across the thickness of the composite wall.View Solution
Knowledge Check
- Question 1 - Select One
1.56×105J of heat is conducted through is 2m2 wall of 12 cm thick in one hour. Temperature difference between the two sides of the wall is 20∘C. The thermal conductivity of the material of the wall is (in Wm−1K−1)
A0.11B0.13C0.15D1.2 - Question 2 - Select One
1.56×105J of heat is conducted through is 2m2 wall of 12 cm thick in one hour. Temperature difference between the two sides of the wall is 20∘C. The thermal conductivity of the material of the wall is (in Wm−1K−1)
A0.11B0.13C0.15D1.2 - Question 3 - Select One
The graph shown gives the temperature along an X axis that extends directly through a wall consisting of three layers A, B and C. The air temperature on one side of the wall is 150∘C and on the other side is 80∘C. Thermal conduction through the wall is steady. out of the three layers A B and C thermal conductivity is greatest of the layer
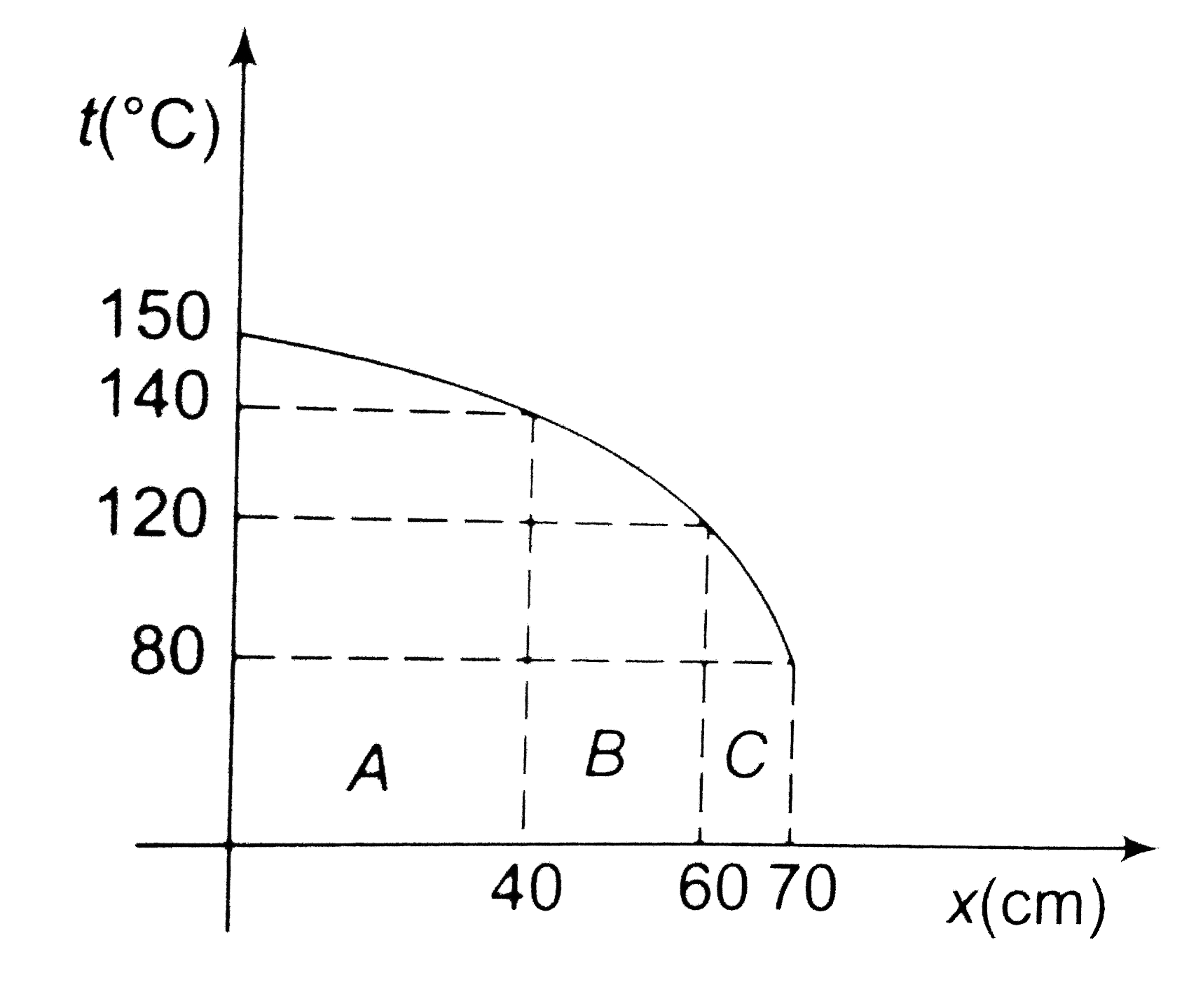 AABBCCDThermal conductivity of A = Thermal conductivity of B.
AABBCCDThermal conductivity of A = Thermal conductivity of B.
(a) Calculate the rate at which body heat is conducted through the clothing of a skier in a steady-state process, given the following data: the body surface area is 1.8m2, and the clothing is 1.0 cm thick , the skin surface temperature is 33∘C and the outer surface of the clothing is at 1.0∘C, the thermal conductivity of the clothing is 0.040W/m.K. (b) If , after a fall, the skier's clothes became soaked with water of thermal conductivity 0.60W/m.K, by how much is the rate of conduction multiplied ?
View SolutionA steel bar 10.0 cm long is welded end to end to a copper bae 20.0 cm long. Both bars are insulated perfectly on their sides . Each bar has a separate cross-section, 2.00 cm on a side . The free end of the steel bar is maintained at 100∘C by placing it in contact with ice . find the temperature at the junction of the two bars and the total rate of heat flow . thermal conductivity of steel =50.2Wm−1K−1.thermal conductivity of copper =385Wm−1K−1.
View SolutionAn iron boiler with walls 1.25cm thick contains water at atmospheric pressure. The heated surface is 2.5m2 in ara and the temperature of the underside is 120∘C. Thermal conductivity of iron is 20cals−1m−1K−1 and the latent heat of evaporatioin of water 536×103calkg−1 (J=4.2Jcal−). Find the mass of water evaporated per hour.
View SolutionThe graph shown gives the temperature along an X axis that extends directly through a wall consisting of three layers A, B and C. The air temperature on one side of the wall is 150∘C and on the other side is 80∘C. Thermal conduction through the wall is steady. Out of the three layers A B and C, thermal conductivity is greatest of the layer
 View Solution
View SolutionIf the temperature difference on the two sides of a wall increases from 100∘C to 200∘C, its thermal conductivity
View Solution

