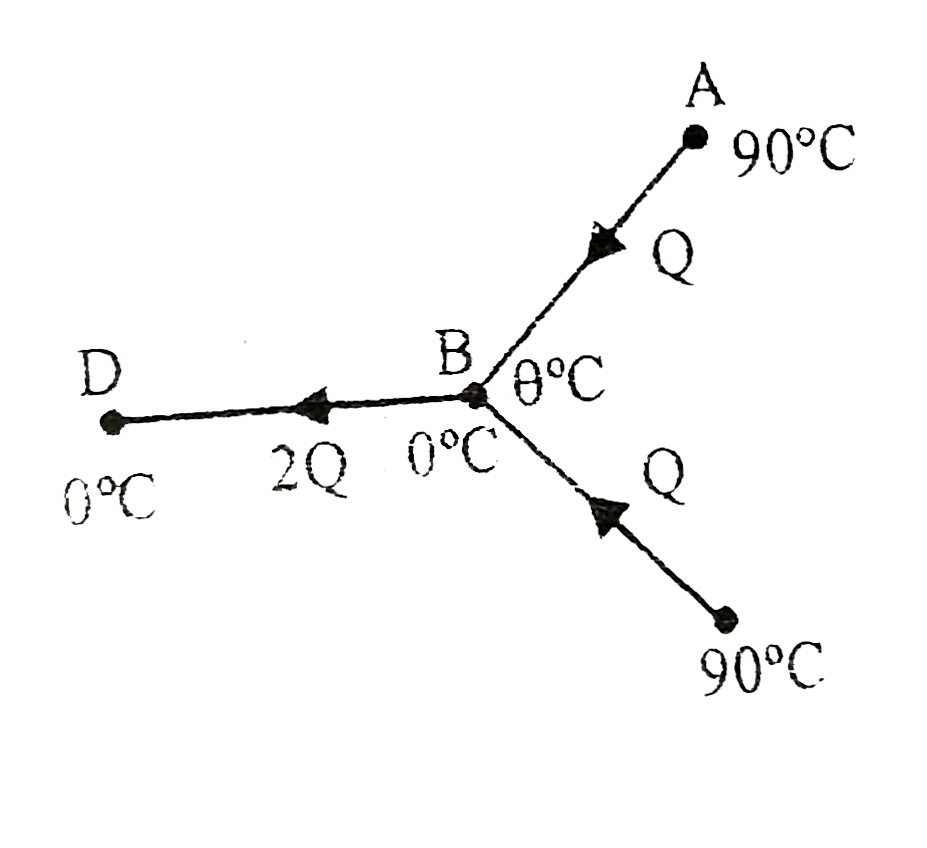
If emissivity of bodies $X$ and $Y$ are $e_{x}$ and $e_{y}$ and absorptive power are $A_{x}$ and $A_{y}$ then

A

$e_{y} > e_{x}$ , $A_{y} > A_{x}$

B

$e_{y} < e_{x}$ , $A_{y} < A_{x}$

C

$e_{y} > e_{x}$ , $A_{y} < A_{x}$

D

$e_{y} = e_{x}$ , $A_{y} = A_{x}$

Text Solution

Verified by Experts

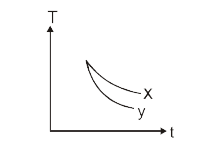
$(A)$ The graph shows that the the same temperature difference $(T_{2} - T_{1})$ , less is taken for $x$ . This means the emissivity is more for $x$ . According to Kirchoff's law, a good emitter is a good absorber as well.

|

Updated on:21/07/2023

Class 11 PHYSICS THERMAL EXPANSION AND CALORIMETRY

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
Relation between emissivity e and absorptive power a is (for black body)
A $e = a$
B $e = \frac{1}{a}$
C $e = a^{2}$
D $a = e^{2}$
Question 2 - Select One
In a compound $A_{x} B_{y}$ :
AMole of $A = Mole of B = Mole of A_{x} B_{y}$
BEq. of $A = E q . of B = E q . of A_{x} B_{y}$
C $y \times mole of A = y \times mole of B = (x + y) \times mole of A_{x} B_{y}$
D $y \times mole of A = y \times mole of B$
Question 3 - Select One
In a compound $A_{x} B_{y}$
Amoles of A = moles of B = moles of $A_{x} B_{y}$
Beq.of A = eq of B = eq.of $A_{x} B_{y}$
Cy $\times$ moles of A = y $\times$ moles of B = $(x + y) \times$ moles of $A_{x} B_{y}$
Dy $\times$ moles of A = y $\times$ moles of B

BANSAL-HEAT TRANSFER-Exercise

Home
Ask Doubt
Profile