While the piston is at a distance 2L from the top, the hole at the top is sealed. The piston is then released, to a poistion where it can stay in equilibrium. In this condition, distance of the piston from the top is
2P0ϕ2ϕr2P0+Mg(2L)
P0ϕR2−MgϕR2P0(2L)
P0ϕR2+Mgϕr2P0(2L)
P0ϕR2ϕR2P0−Mg(2L)
The correct Answer is:C
Topper's Solved these Questions
- KINETIC THEORY OF GASESBOOK - BANSALCHAPTER - KINETIC THEORY OF GASESEXERCISE - Section-B
13 Videos
- KINETIC THEORY OF GASESBOOK - BANSALCHAPTER - KINETIC THEORY OF GASESEXERCISE - Exercise-3
33 Videos
- HEAT TRANSFERBOOK - BANSALCHAPTER - HEAT TRANSFEREXERCISE - Exercise
89 Videos
- UNIT DIMENSION, VECTOR & BASIC MATHSBOOK - BANSALCHAPTER - UNIT DIMENSION, VECTOR & BASIC MATHSEXERCISE - Exercise
10 Videos
Similar Questions
A fixed thermally conducting cylinder has a radius R and height L0. The cylinder is open at its bottom and has a small hole at its top. A piston of mass M is held at a distance L from the top surface, as shown in the figure. The atmospheric pressure is P0.
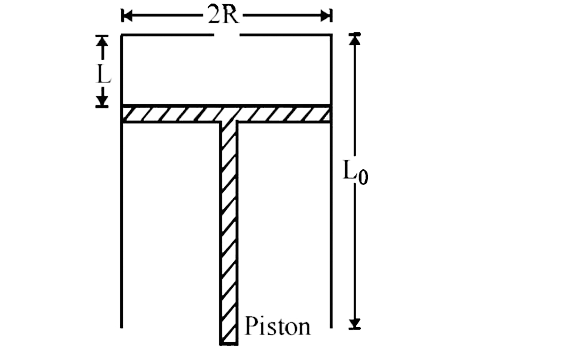
While the piston is at a distance 2L from the top, the hole at the top is sealed. The piston is then released, to a position where it can stay in equilibrium. In this condition, the distance of the piston from the top is
View SolutionFollowing figure shows on adiabatic cylindrical container of volume V0 divided by an adiabatic smooth piston (area of cross-section = A ) in two equal parts. An ideal gas (Cp/Cy=λ) is at pressure P1 and temperature T1 in left part and gas at pressure P2 and temperature T2 in right part. The piston is slowly displaced and released at a position where it can stay in equilibrium. The final pressure of the two parts will be (Suppose x = displacement of the piston)

View Solution
Knowledge Check
A fixed thermally conducting cylinder has a radius R and height L0. The cylinder is open at ita bottom and has a small hole at its top. A piston of mass M is held at a distance L from the top surface, as shown in the figure. The atmospheric pressure is P0.

While the piston is at a distance 2L from the top, the hole at the top is sealed. The piston is then released, to a position where it can stay in equilibrium. In this condition, the distance of the piston from the top isA(2P0πR2πR2P0+Mg)(2L)B(P0πR2−MgπR2P0)(2L)C(P0πR2+MgπR2P0)(2L)D(P0πR2πR2P0−Mg)(2L)A fixed thermally conducting cylinder has radius R and length L0. The cylinder is open at its bottom and has a small hole at its top. A piston of mass M is held at a distance L from the top surface, as shown in the figure. The atmospheric pressure is P0.
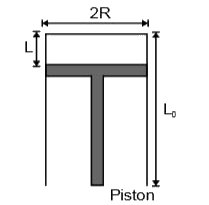
While the piston is at a distance 2L from the top, the hole at the top is sealed. The piston is then released, to a position where it can stay in equilibrium. In this condition, the distance of the piston from the top isA(2P0πR2πR2P0+Mg)(2LB(p0πR2−MgπR2P0)(2L)C(p0πR2+MgπR2P0)(2L)D(P0πr2πR2P0−Mg)(2L)Following figure shows on adiabatic cylindrical container of volume V0 divided by an adiabatic smooth piston (area of cross-section = A ) in two equal parts. An ideal gas (Cp/Cy=λ) is at pressure P and temperature T in left part and gas at pressure P and temperature T in right part. The piston is slowly displaced and released at a position where it can stay in equilibrium. The final pressure of the two parts will be (Suppose x = displacement of the piston)
 AP2BP1CP1(V02)λ(V02+Ax)λDP2(V02)λ(V02+Ax)λ
AP2BP1CP1(V02)λ(V02+Ax)λDP2(V02)λ(V02+Ax)λ
A fixed thermally conducting cylinder has a radius R and height L0. The cylinder is open at the bottom and has a small hole at its top. A piston of mass M is held at a distance L from the top surface, as shown in the figure. The atmospheric pressure is P0.
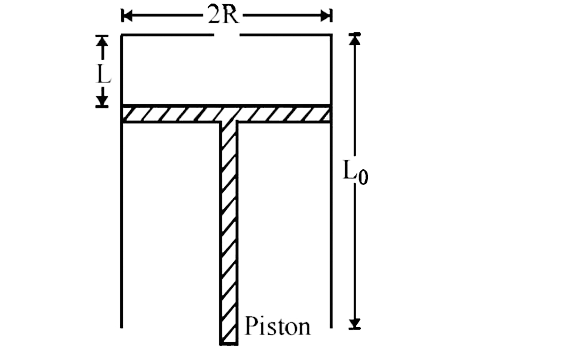
The piston is now pulled out slowly and held at a distance 2L from the top. The pressure in the cylinder between its top and the piston will then be
View SolutionAn ideal gas is enclosed in a cylinder having cross sectional area A. The piston of mass M has its lower face inclined at θ to the horizontal. The lower face of the piston also has a hemispherical bulge of radius r. The atmospheric pressure is P0.
(a) Find pressure of the gas.
(b) The piston is slowly pulled up by a distance x. During the process the piston is always maintained in equilibrium by adding heat to the gas. [It means if the piston is left at any stage it will stay there in equilibrium]. Find change in temperature of the gas. Number of mole of the gas in the cylinder is one.

View SolutionAn observer from point on the ground Views the top of the tower AB, such that its distance from the tower height ofthe tower and distance between top of the tower and point Con the ground are in AP and their sum is 12. The tangent of ange of elevation of the top of the tower from point Cis
View SolutionA fixed thermally conducting cylinder has a radius R and height L0. The cylinder is open at ita bottom and has a small hole at its top. A piston of mass M is held at a distance L from the top surface, as shown in the figure. The atmospheric pressure is P0.

The piston is now pulled out slowly and held at a distance 2L from the top. The pressure in the cylinder between its top and the piston will then be
View SolutionThe piston is taken completely out of the cylinder. The hole at the top is sealed. A water tank is brough below the cylinder and put in a positoon so that the water surface in the tank is at the same level as the top of the cylinder as shown in the fgure. The density of the water is rho.In equilibriium, the height H of the water column in the cylinder satisfies

View Solution
