The piston is taken completely out of the cylinder. The hole at the top is sealed. A water tank is brough below the cylinder and put in a positoon so that the water surface in the tank is at the same level as the top of the cylinder as shown in the fgure. The density of the water is rho.In equilibriium, the height H of the water column in the cylinder satisfies
ρg(L0−H)2+P0(L0−H)+(L0P0)=0
ρg(L0−H)2−P0(L0−H)−L0P0=0
ρg(L0−H)2+P0(L0−H)−L0P0=0
ρ(L0−H)2−P0(L0−H)+(L0P0)=0
The correct Answer is:C
Topper's Solved these Questions
- KINETIC THEORY OF GASESBOOK - BANSALCHAPTER - KINETIC THEORY OF GASESEXERCISE - Section-B
13 Videos
- KINETIC THEORY OF GASESBOOK - BANSALCHAPTER - KINETIC THEORY OF GASESEXERCISE - Exercise-3
33 Videos
- HEAT TRANSFERBOOK - BANSALCHAPTER - HEAT TRANSFEREXERCISE - Exercise
89 Videos
- UNIT DIMENSION, VECTOR & BASIC MATHSBOOK - BANSALCHAPTER - UNIT DIMENSION, VECTOR & BASIC MATHSEXERCISE - Exercise
10 Videos
Similar Questions
Knowledge Check
A fixed thermally conducting cylinder has a radius R and height L0. The cylinder is open at ita bottom and has a small hole at its top. A piston of mass M is held at a distance L from the top surface, as shown in the figure. The atmospheric pressure is P0.
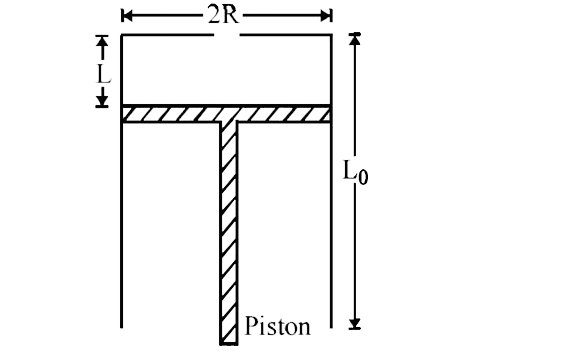
The piston is taken completely out of the cylinder. The hole at the top is sealed. A water tank is brought below the cylinder and put in a position so that the water surface in the tank is at the same level as the top of the cylinder as shown in the figure. The density of the water is ρ. In equilibrium, the height H of the water coulmn in the cylinder satisfies
 Aρg(L0−H)2+P0(L0−H)+L0P0=0Bρg(L0−H)2−P0(L0−H)−L0P0=0Cρg(L0−H)2+P0(L0−H)−L0P0=0Dρg(L0−H)2−P0(L0−H)+L0P0=0
Aρg(L0−H)2+P0(L0−H)+L0P0=0Bρg(L0−H)2−P0(L0−H)−L0P0=0Cρg(L0−H)2+P0(L0−H)−L0P0=0Dρg(L0−H)2−P0(L0−H)+L0P0=0A cylindrical tank has a hole of diameter 2r in its bottom. The hole is covered wooden cylindrical block of diameter 4r, height h and density ρ/3.

Situation I: Initially, the tank is filled with water of density ρ to a height such that the height of water above the top of the block is h1 (measured from the top of the block).
Situation II: The water is removed from the tank to a height h2 (measured from the bottom of the block), as shown in the figure. The height h2 is smaller than h (height of the block) and thus the block is exposed to the atmosphere.
Find the height of the water level h2 (in situation 2), for which the block remains in its origin) position whithout the application of any external forceA∣∣2P0Rh+πR2ρgh−2RT∣∣B∣∣2P0Rh+Rρgh2−2RT∣∣C∣∣P0πR2+Rρgh2−2RT∣∣D∣∣P0πR2+Rρgh2−2RT∣∣Two holes are made in the side of the tank such that the jets of water flowing out of them meet at the same point on the ground. If one hole is at a height of 3cm above the bottom, then the distance of the other holes from the top surface of water is
A32cmB√6cmC√3cmD3cm
A cylindrical tank has a hole of diameter 2r in its bottom. The hole is covered wooden cylindrical block of diameter 4r, height h and density ρ/3.

Situation I: Initially, the tank is filled with water of density ρ to a height such that the height of water above the top of the block is h1 (measured from the top of the block).
Situation II: The water is removed from the tank to a height h2 (measured from the bottom of the block), as shown in the figure. The height h2 is smaller than h (height of the block) and thus the block is exposed to the atmosphere.
In situation 2, if h2 is further decreased, then
View SolutionA tank of height H and base area A is half filled with water and there is a small orifice at the bottom and there is a heavy solid cylinder having base area A3 and height of the cylinder is same as that of the tak. The water is flowing out of the orifice. Here cylinder is put into the tank to increase the speed of water flowing out.
After long time, when the height of water inside the tank again becomes equal to H2, the solid cylinder is taken out. then the velocity of liquid flowing out of the orifice (just after removing the cylinder) will be
View SolutionA cylindrical tank has a hole of diameter 2r in its bottom. The hole is covered wooden cylindrical block of diameter 4r, height h and density ρ/3.

Situation I: Initially, the tank is filled with water of density ρ to a height such that the height of water above the top of the block is h1 (measured from the top of the block).
Situation II: The water is removed from the tank to a height h2 (measured from the bottom of the block), as shown in the figure. The height h2 is smaller than h (height of the block) and thus the block is exposed to the atmosphere.
In situation 2, if h2 is further decreased, then
View SolutionA tank of height H and base area A is half filled with water and there is a small orifice at the bottom and there is a heavy solid cylinder having base area A3 and height of the cylinder is same as that of the tak. The water is flowing out of the orifice. Here cylinder is put into the tank to increase the speed of water flowing out.
After long time, when the height of water inside the tank again becomes equal to H2, the solid cylinder is taken out. then the velocity of liquid flowing out of the orifice (just after removing the cylinder) will be
View SolutionA tank of height H and base area A is half filled with water and there is a small orifice at the bottom and there is a heavy solid cylinder having base area A3 and height of the cylinder is same as that of the tak. The water is flowing out of the orifice. Here cylinder is put into the tank to increase the speed of water flowing out.
The speed of water flowing out of the orifice after the cylinder is kept inside it is
View Solution
