In meter bridge , the balancing length from left is found to be 20 cm when standard connected of 1Ω is in right gap . The value of unknown resistance is
0.25Ω
0.4Ω
0.5Ω
4Ω
The correct Answer is:A
To solve the problem, we will use the principles of a meter bridge and the concept of balancing lengths.
1. Understanding the Meter Bridge Setup:
- A meter bridge consists of a wire of length 1 meter (100 cm) that is used to compare two resistances.
- When the bridge is balanced, the ratio of the resistances is equal to the ratio of the lengths from the jockey to the ends of the bridge.
2. Identifying Given Values:
- The balancing length from the left (let's call it L1) is given as 20 cm.
- The standard resistance (Rs) connected in the right gap is 1 ohm.
- The remaining length from the jockey to the right end (let's call it L2) can be calculated as:
L2=100cm−L1=100cm−20cm=80cm
3. Setting Up the Balance Equation:
- According to the meter bridge principle, the ratio of the resistances is equal to the ratio of the lengths:
RxRs=L2L1
- Here, Rx is the unknown resistance we need to find.
4. Substituting the Known Values:
- Substitute Rs=1Ω, L2=80cm, and L1=20cm into the equation:
Rx1=8020
5. Calculating the Unknown Resistance:
- Simplifying the right side:
Rx=8020=4Ω
Final Answer:
The value of the unknown resistance Rx is 4 ohms.
---
- A meter bridge consists of a wire of length 1 meter (100 cm) that is used to compare two resistances.
- When the bridge is balanced, the ratio of the resistances is equal to the ratio of the lengths from the jockey to the ends of the bridge.
- The balancing length from the left (let's call it L1) is given as 20 cm.
- The standard resistance (Rs) connected in the right gap is 1 ohm.
- The remaining length from the jockey to the right end (let's call it L2) can be calculated as:
L2=100cm−L1=100cm−20cm=80cm
- According to the meter bridge principle, the ratio of the resistances is equal to the ratio of the lengths:
RxRs=L2L1
- Here, Rx is the unknown resistance we need to find.
- Substitute Rs=1Ω, L2=80cm, and L1=20cm into the equation:
Rx1=8020
- Simplifying the right side:
Rx=8020=4Ω
The value of the unknown resistance Rx is 4 ohms.
Topper's Solved these Questions
Similar Questions
Resistance of a wire is, measured using a meter bridge and the balancing length for the unknown resistance of 10ω in the right gap is 48 cm. Find the value of the resistance. If the end corrections are 0.6 cm and 0.4 cm respectively for the left and right ends, find the corrected value of the unknown resistance.
View Solution(i) In a meter bridge , the balance point is found to be at 30cm from the end A when resistance R in left gap of bridge is of 12Ω. Find resistance S in the right gap of bridge
(ii) If the cell and the galvanometer are interchanged in the balance point, would it effect flow of current through the galvanometer
(iii) Calculate the balance point of the bridge if R and S are interchanged
View Solution
Knowledge Check
In a metre bridge , the balancing length from the left end is found to be 40cm, when a known resistance of 3Ω is placed in the right gap, then the value of unknown resistance is
A1ΩB2ΩC3ΩD4ΩIn a metre bridge experiment, the balancing length from the left end is found to be 20 cm. If a standard resistance of 20 ohm is kept in the right gap, then the value of the unknown resistance in the left gap is
A5ΩB10ΩC15ΩD7.5ΩIn a meter bridge , the balancing length from left end ( standard resistance of one ohm is in the right gap ) is found to be 20 cm . The value of the unknow resistance is .
A0.25ΩB0.8ΩC0.2ΩD0.16Ω
In a metere bridge, the balance length from left end (standard resistance of 1Ω is in the right gap) is found to be 20 cm, the length of resistance wire in left gap) is found to be 20 cm the length of resistance wire in left gap is 12 m and radius is 2mm its specific resistance is
View SolutionIn the metre bridge, the balancing length AB = 20 cm. The unknown resistance X is equal to
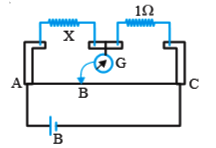
View SolutionWhen an unknown resistance and a resistance 6Ω are connected in the left and right gaps of a meter bridge the balance point is obtained at 50 cm. if 3Ω resistance is connected in parallel to resistance in right gap, the balance point is
View SolutionWhen an unknown resistance and a resistance of 4Ω are connected in the left and right gaps of a meterbridge, the balance point is obtained at 50 cm. the shift in the balance point if a 4Ω resistance is now connected in parallel to the resistance in the right gap is
View SolutionConsider a metre bridge whose length of wire is 2m. A resistance of 10Ω is connected across one gap of the meter bridge and an unknown resistance is connected across the other gap. When these resistances are interchanged, the balance point shifts by 50 cm. What is the value of the unknown resistance?
View Solution
