The bottom of the legs of a three legged table are the vertices of an isosceles triangle with sides 5, 5 and 6. The legs are to be braced at the bottom by three wires in the shape of a Y. The minimum length of the wire needed for this purpose, is
4+3√3
10
3+4√3
1+6√2
The correct Answer is:A
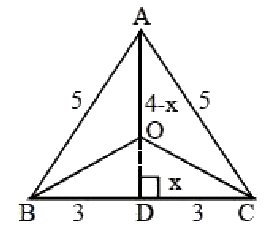
l=4−x+2√9+x2
dldx=−1+2√9+x2
dldx=0
⇒x=√3
d2ldx2=18√9+x2>0, for x=√3
∴lmin=4−√3+√9+3
=4+3√3.
Similar Questions
The bottom of the legs of a three legged table are the vertices of an isoceless triangle with side legs are to be braced at the bottom by three wires in the shape of a Y. The minimum length of wire needed for this purpose, is
View SolutionFind the area of an isosceles triangle having the base 6 cm and the length of each equal side 5 cm.
View Solution
Knowledge Check
- Question 1 - Select One
The number of values of b for which there is an isoscles triangle with sides of length b+5,3b−2, and 6−b is:
A0B1C2D3 - Question 2 - Select One
The lengths of the sides of an isosceles triangle are in the ratio 3:3:5. The length of the equal sides of the triangle is 6.6 cm. What is the perimeter of the triangle ?
A23.5cmB24.0cmC24.2cmD25.0cm
Two vertices of an isosceles triangle are (2, 0) and (2, 5) . Find the third vertex if the length of the equal sides is 3.
View SolutionShow that A(6,4),B(5,−2)andC(7,−2) are the vertices of an isosceles triangle. Also, find the length of the median through A.
View SolutionA piece of wire 78 cm long is bent in the form of an isosceles triangle. If the ratio of one of the equal sides to the base is 5:3, then what is the length of the base ?
View SolutionThree masses of 1 kg each are kept at the vertices of an equilateral triangle of side 3 m. What is the force acting on a point mass of 5 kg placed at its centroid ?
View SolutionThree balls each of mass 0.5 kg are kept at the vertices of an isosceles right triangle with its hypotenuse of 2√2 m. What will be the net gravitational force on the ball kept at the vertex of right angle ?
View SolutionFind the equation of the legs of a right isosceles triangle if the equation of its hypotenuse is x−2y−3=0 and the vertex of the right angle is at the point (1,6),
View Solution

