A wheel rolls without slipping on a horizontal surface such that its velocity of center of mass is v. The velocity of a particle at the highest point of the rim is
zero
v
2v
√2v
When a body rolls without slipping, the velocity of any point of the body is resultant of two velocities: one due to pure translational motion and another due to pure rotational motion. Also, v=rω.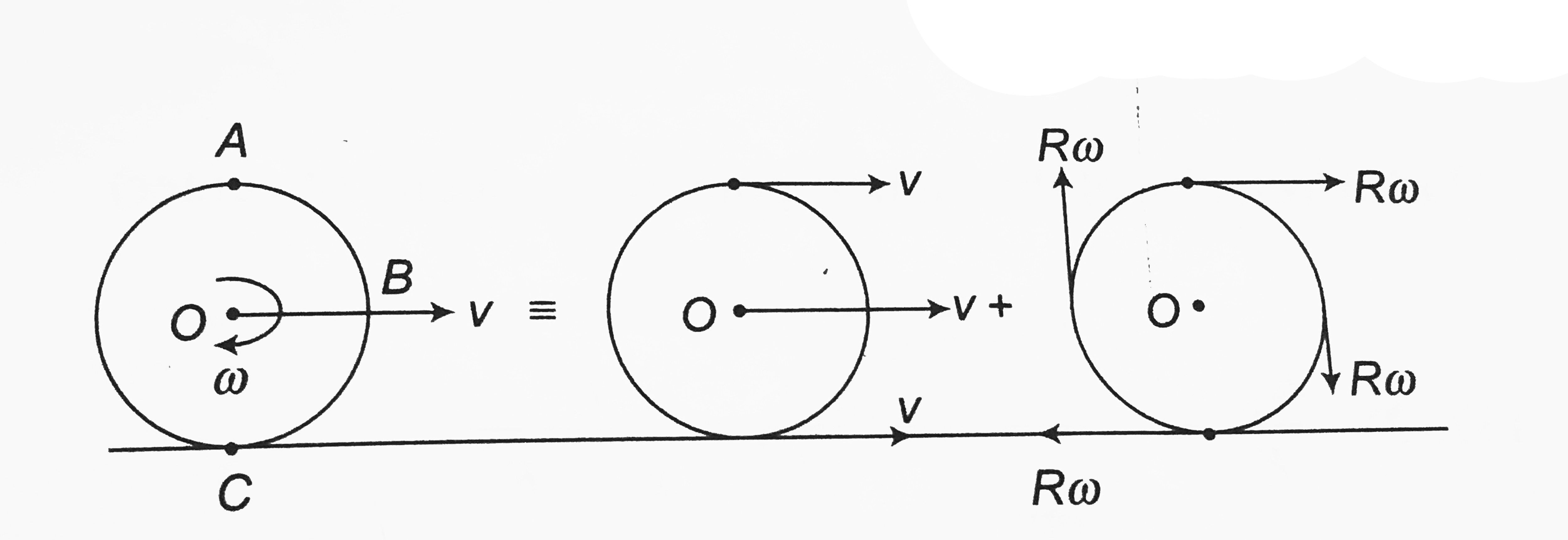 
vA=v+Rω=v+v=2v
vB=√v2+(rω)2=√2v
vC=v−v=0
Topper's Solved these Questions
Similar Questions
A disc rolls without slipping on a horizontal surface such that its velocity of center of the mass is v. Find the velocity of points A,B,C and D.
View SolutionA solid sphere of mass m and radius R rolls without slipping on the horizontal surface such that its velocity of center of mass is v0. Find its translational kinetic energy, rotational kinetic energy, total kinetic energy, gravitational potential energy taking surface as reference level and mechanical energy.
View Solution
Knowledge Check
- Question 1 - Select One
Assertion: A disc rolls without slipping on a horizontal surface and the linear speed of its centre of mass is v. The rotational speed of the particles on its rim at the top of the disc will be 2v.
Reason: The disc rolls as if it is rotating about the point of contact with the horizontal surface.AAssertion is True, Reason is True, Reason is a correct explanation for AssertionBAssertion is True, Reason is True, Reason is not a correct explanation for AssertionCAssertion is False but, Reason is True.DAssertion is True, Reason is False - Question 2 - Select One
If the velocity of centre of mass of a rolling body is V then velocity of highest point of that body is
A√2VBVC2VDV√2 - Question 3 - Select One
If V is velocity of centre of mass of a rolling body then velocity of lowest point of that body is
A√2VBVC2VDzero
A hollow sphere rolls without slipping the on the horizontal surface such that its translational velocity is v. Find that the maximum height attained by it on an inclined surface.
View SolutionA ball of radius R and mass m is rolling without slipping on a horizontal surface with velocity of its centre of mass vCM. It then rolls wilthout slippig up a hill to a height h before momentarily coming to rest. Find h
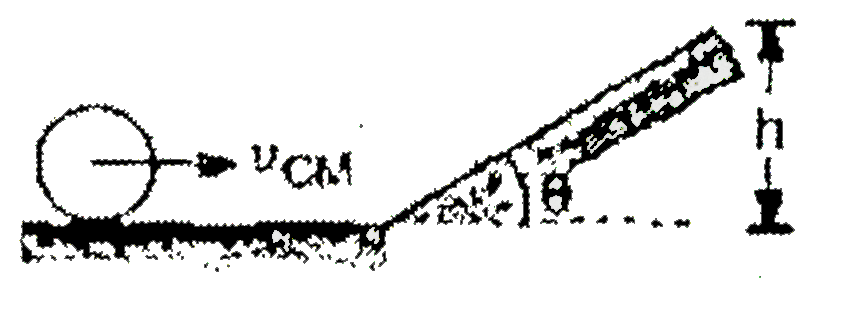View SolutionA bobbin rolls without slipping over a horizontal surface so that the velocity v of the end of the thread (point A) is directed along the horizontal . A board hinged at point B leans against the bobbin (Fig.) The inner and outer radii of the bobbin are r and R respectively. Determine the angular velocity ω of teh board as a function of an angle α.
View SolutionA disc of radius r rolls without slipping on a rough horizontal floor. If veloocity of its centre of mass is v0, then velocity of point P, as shown in the figure
(OP=r/2 and ∠QOP=60∘)is
View SolutionA uniform circular disc of mass M and radius R rolls without slipping on a horizontal surface. If the velocity of its centre is v0, then the total angular momentum of the disc about a fixed point P at a height (3R)/2 above the centre C.
View Solution