A block of 1 kg is stopped against a wall by applying a force F perpendicular to the wall. If then minimum value of F will be
980 N
49 N
98 N
490 N
The correct Answer is:B
To solve the problem of finding the minimum force F required to stop a block of mass 1kg against a wall, given that the coefficient of friction μ=0.2, we can follow these steps:
Step 1: Identify the Forces Acting on the Block
The forces acting on the block are:
- The gravitational force mg acting downwards.
- The applied force F acting perpendicular to the wall.
- The frictional force f acting upwards (which prevents the block from falling).
Step 2: Calculate the Weight of the Block
The weight mg of the block can be calculated using:
mg=1kg×9.8m/s2=9.8N
Step 3: Understand the Role of Friction
The frictional force f that acts upwards can be expressed in terms of the normal force N (which is equal to the applied force F in this case):
f=μN=μF
Since the block is not falling, the frictional force must balance the weight of the block:
f≥mg
Step 4: Set Up the Inequality
Substituting the expression for friction into the inequality gives:
μF≥mg
This can be rewritten as:
F≥mgμ
Step 5: Substitute the Known Values
Now, substituting the known values of mg and μ:
F≥9.8N0.2
Step 6: Calculate the Minimum Force
Calculating the right-hand side:
F≥9.80.2=49N
Conclusion
Thus, the minimum value of the force F required to prevent the block from falling is:
49N
The forces acting on the block are:
- The gravitational force mg acting downwards.
- The applied force F acting perpendicular to the wall.
- The frictional force f acting upwards (which prevents the block from falling).
The weight mg of the block can be calculated using:
mg=1kg×9.8m/s2=9.8N
The frictional force f that acts upwards can be expressed in terms of the normal force N (which is equal to the applied force F in this case):
f=μN=μF
Since the block is not falling, the frictional force must balance the weight of the block:
f≥mg
Substituting the expression for friction into the inequality gives:
μF≥mg
This can be rewritten as:
F≥mgμ
Now, substituting the known values of mg and μ:
F≥9.8N0.2
Calculating the right-hand side:
F≥9.80.2=49N
Thus, the minimum value of the force F required to prevent the block from falling is:
49N
Topper's Solved these Questions
Similar Questions
A block of mass 1kg is pressed against a wall by applying a horizontal force of 10N on the block. If the coefficient of friction between the block and the wall is 0.5 ,magnitude of the frictional force acting on the block is
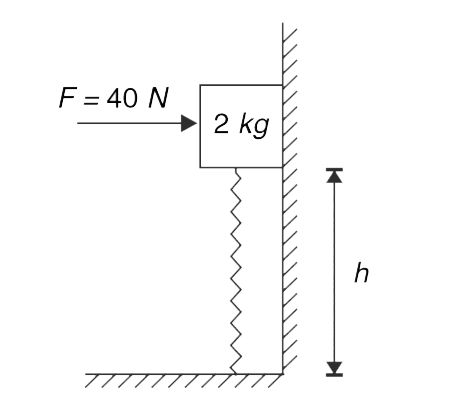
View Solution(i) In the arrangement shown in the figure the coefficient of friction between the 2 kg block and the vertical wall is μ=0.5. A constant horizontal force of 40 N keeps the block pressed against the wall. The spring has a natural length of 1.0 m and its force constant is k=400Nm–1. What should be the height h of the block above the horizontal floor for it to be in equilibrium. The spring is not tied to the block.
(ii) A block of mass M is pressed against a rough vertical wall by applying a force F making an angle of θ with horizontal (as shown in figure). Coefficient of friction between the wall and the block is μ=0.75.
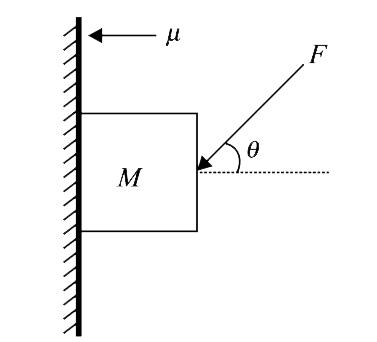
(a) If F = 2 Mg, find the range of values of θ so that the block does not slide
[Take tan37∘=0.75,sin24∘=0.4]
(b) Find the maximum value of θ above which equilibrium is not possible for any magnitude of force F.View Solution
Knowledge Check
- Question 1 - Select One
A rectangular block of mass 6 kg is to be held against a rough vertical wall by appplying a force perpendicular to the wall. What is the minimum force to be applied, if the coefficient of friction is 0.42?
A140 NB120 NC100 ND80 N - Question 2 - Select One
A rectangular block of mass 2 kg is to be held against a rough vertical wall by applying a force of 98 N perpendicular to the wall. What is the coefficients of friction if the applied force is the minimum required force?
A0.1B0.15C0.2D0.3 - Question 3 - Select One
A block of mass 0.1 kg is held against a wall by applying a horizontal force of 5 N on the block. If the coefficient of friction between the block and the wall is 0.5, then the magnitude of the frictional force acting on the block is
A2.5 NB0.98 NC4.9 ND0.49 N
A block weighs W is held against a vertical wall by applying a horizontal force F. The minimum value of F needed to hold the block is
View SolutionA rectangular block is held against a vertical wall by applying a force of 200N normal to the wall. If the frictional froce just prevents the block from sliding down the wall, what is the mass of the block? (The coefficient of static friction between the block and the wall is 0.49)
View SolutionA block of mass m is held fixed against a wall by a applying a horizontal force F. Which of the following option is incorrect :
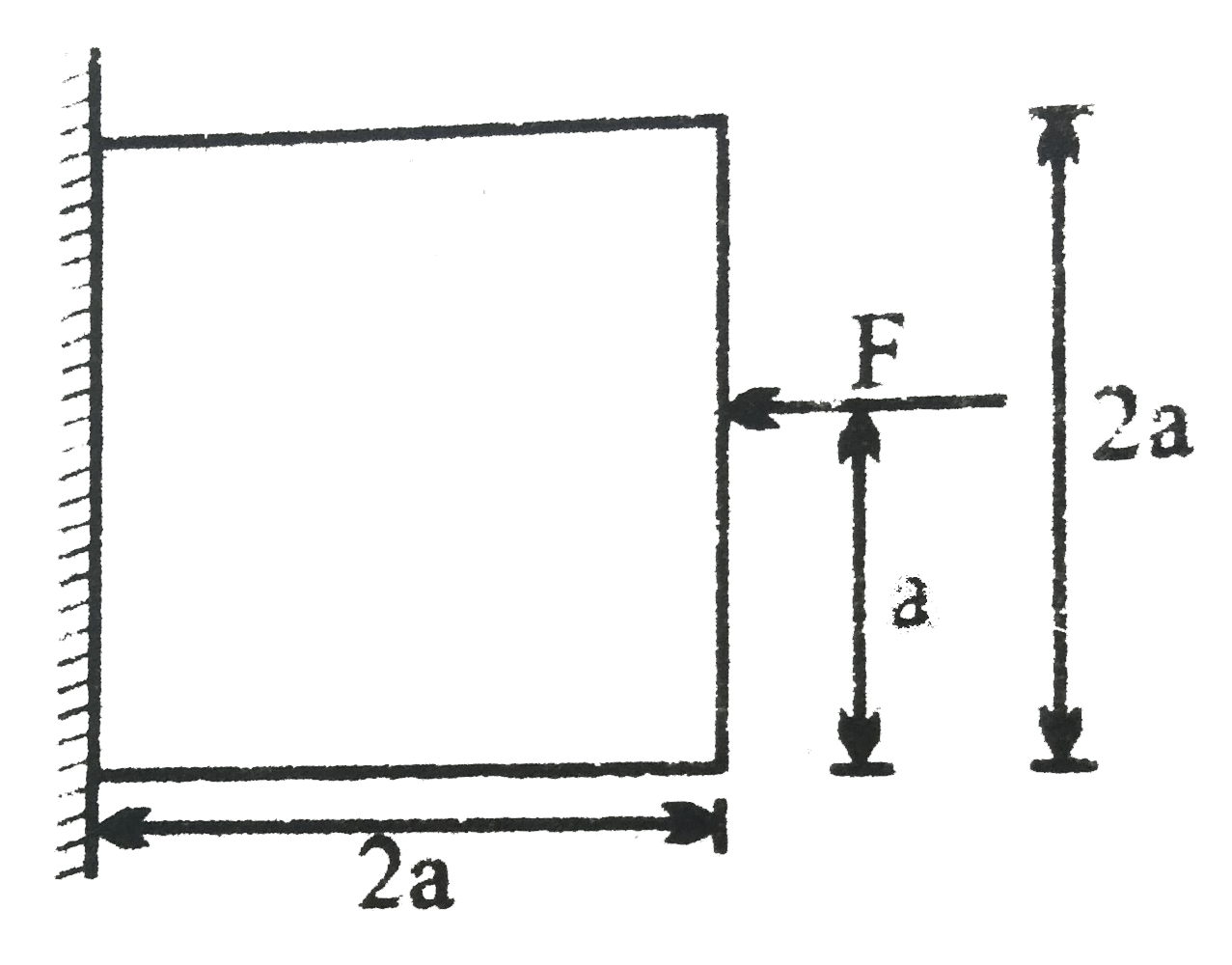 .View Solution
.View SolutionA block of mass 'm' is held stationary against a rough wall by applying a force F as shown. Which one of the following statement is incorrect ?
 View Solution
View SolutionIn the figure shown, a cubical block is held stationary against a rough wall by applying a force F, then. Incorrect statement among the following is :
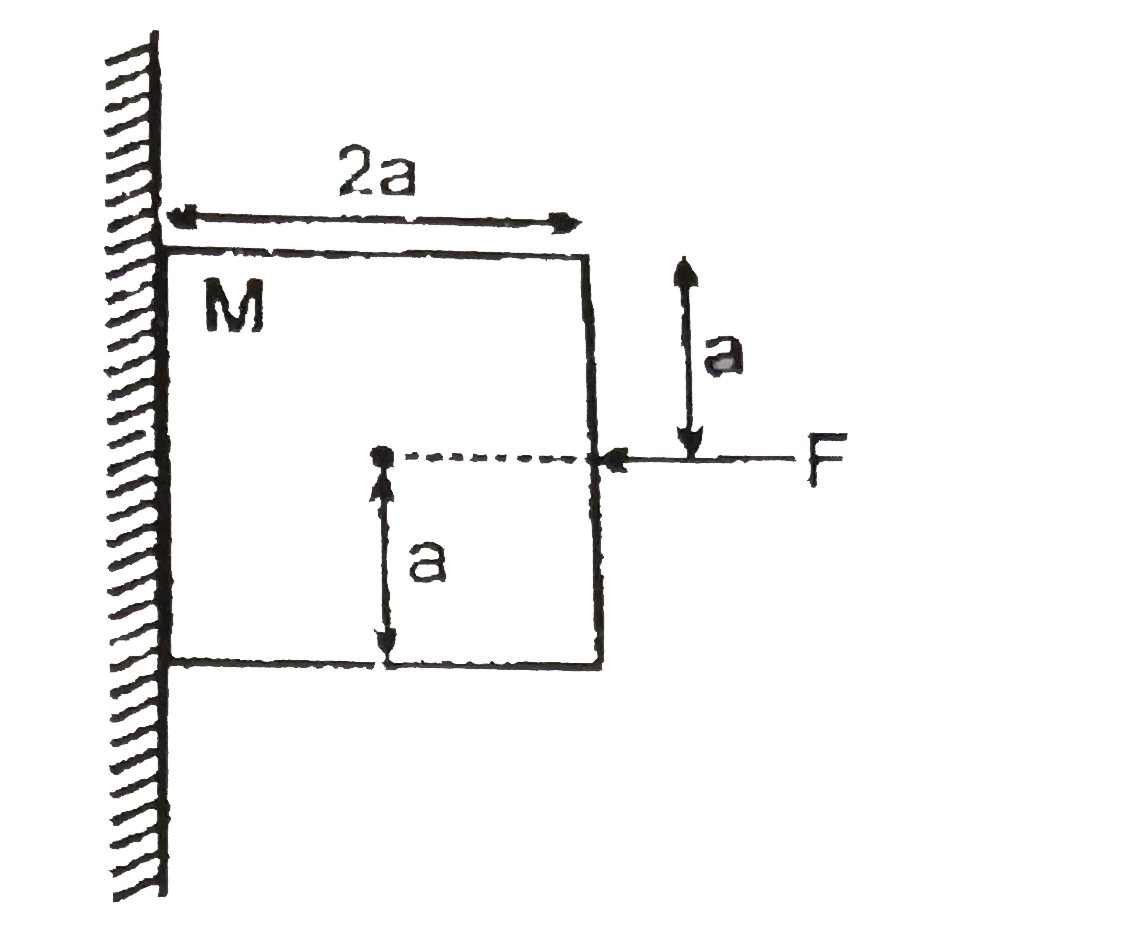 View Solution
View Solution

