Two small identical circular loops marked (1) and (2) carrying equal currents, are placed with their gometrical axes perpendicular to each other as shown in figure. Find the magnitude and direction of the net magnetic field produced at O. Also determine the field when radius of the loop is very large as compared to the distance of the point from centre.
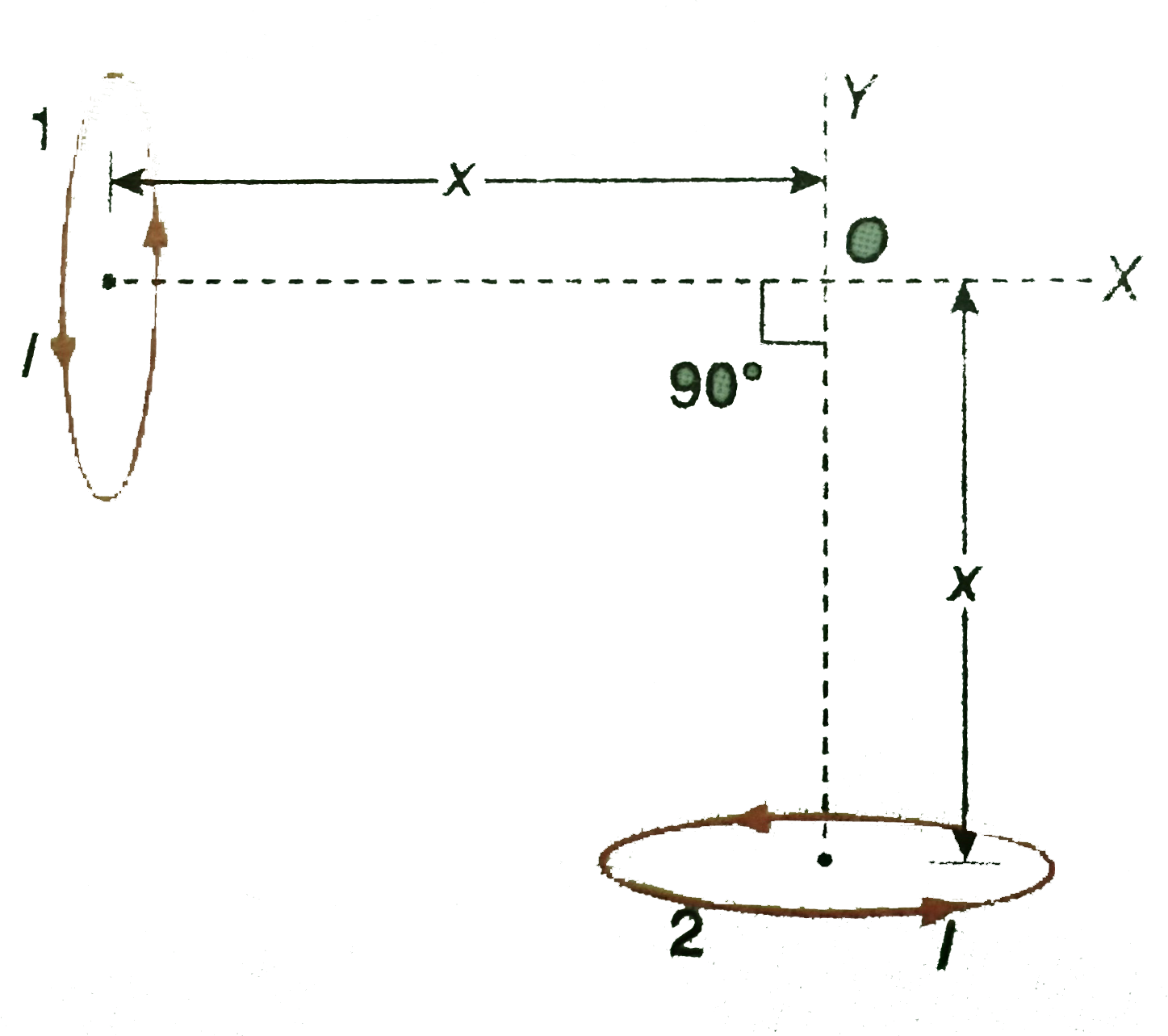
Let R be the radius of each loop. Magnetic field at O due to loop 1,
B1=μ0IR22(R2+x2)3/2(it act along−−→OX)
Magnetic field at O due to loop 2,
B2=μ0IR22(R2+x2)3/2(it acts along−−→OY).
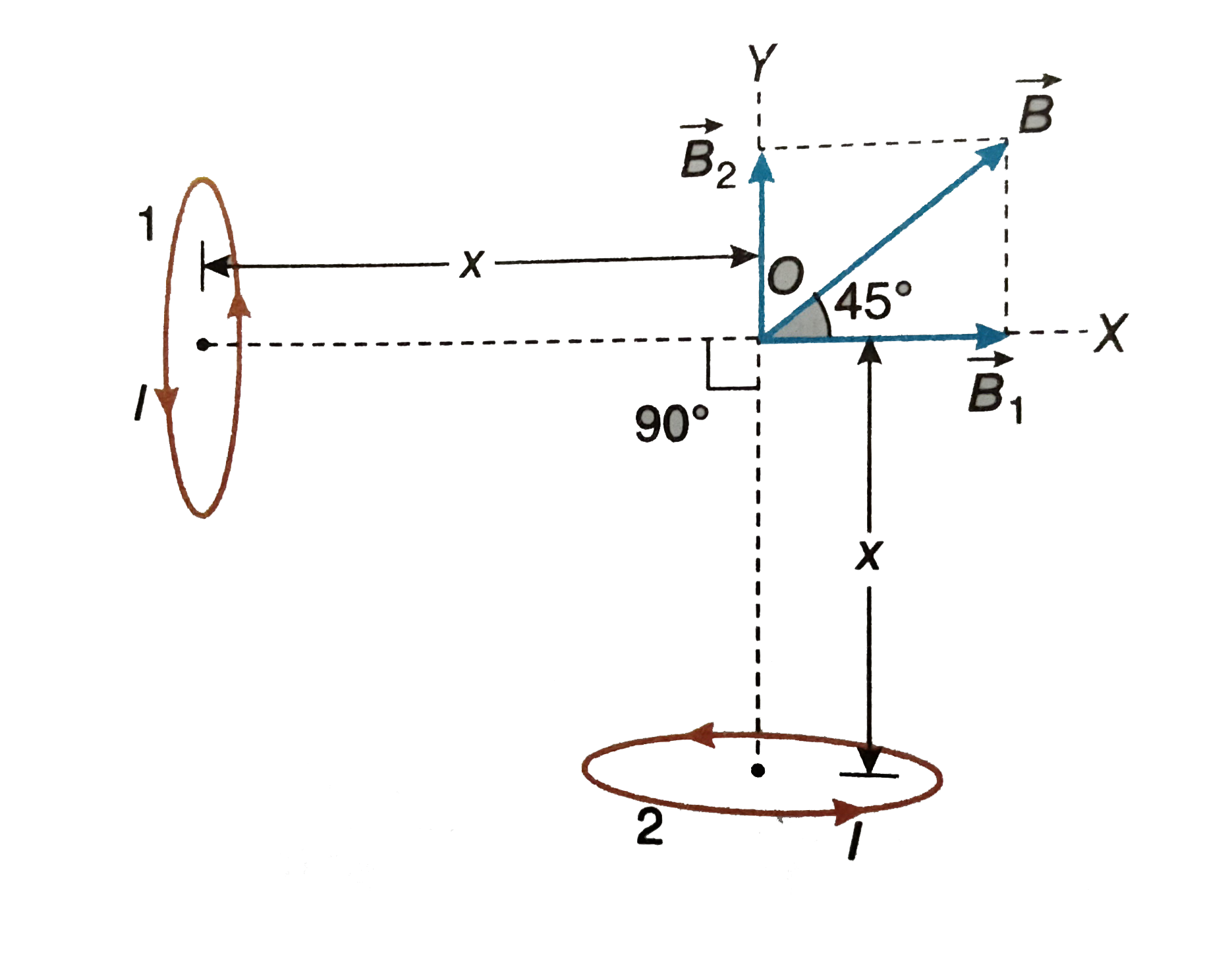
∴ Net magnetical field at O the both the loops,
B=√B21+B22=√2B21=√2B1[∴B1=B2]
This field act at an angle of 45∘ with −−→OX.
Now if R>>x, neglecting x2/R2 we get,
B=μ0IR2√2[R2(1+x2/R2)]3/2≈μ0IR2√2R3
∴B≈μ0I√2R
Topper's Solved these Questions
- ELECTROMAGNETISM BOOK - CHHAYA PUBLICATIONCHAPTER - ELECTROMAGNETISM EXERCISE - SECTION RELATED QUESTIONS
64 Videos
- ELECTROMAGNETISM BOOK - CHHAYA PUBLICATIONCHAPTER - ELECTROMAGNETISM EXERCISE - HIGHER ORDER THINKING SKILL (HOTS) QUESTIONS
48 Videos
- ELECTROMAGNETIC WAVES BOOK - CHHAYA PUBLICATIONCHAPTER - ELECTROMAGNETIC WAVES EXERCISE - CBSE SCANNER
17 Videos
- ELEMENTARY PHENOMENA OF ELECTROSTATICS BOOK - CHHAYA PUBLICATIONCHAPTER - ELEMENTARY PHENOMENA OF ELECTROSTATICS EXERCISE - EXAMINATION ARCHIVE
2 Videos
Similar Questions
What are the fundamental properties of a magnet ?
View SolutionState whether the mutual distances between the circular magnetic lines of force obtained on a plane, perpendicular to a straight long current carrying wire would be the same or not ?
View SolutionWhat are the directions of electric and magnetic field vectors relative to each other and relative to the direction of propagation of electromagnetic waves?
View SolutionDefine surface density of electric charge
View SolutionA part of a long wire carrying a current i is bent into a circle of radius r as shown in figure. The net magnetic field at the centre O of the circular loop is
View SolutionTwo coaxial circular loops L_1 and L_2 of radii 3cm and 4cm are placed as shown in figure. What should be the magnitude and direction of the current in the loop L_2 so that the net magnetic field at the point O be zero?
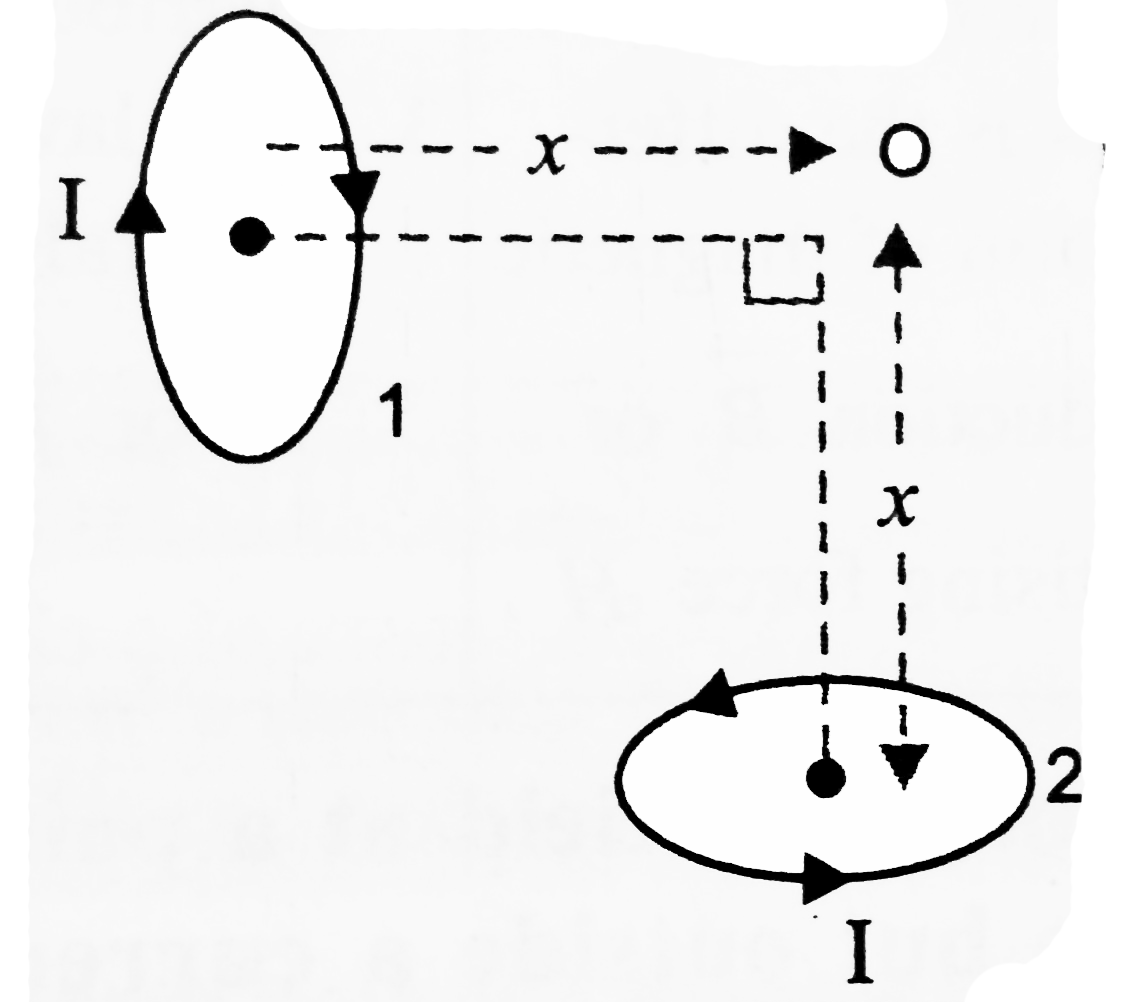
View SolutionTwo small circular loops, marked (1) and (2), carrying equal currents are placed with the geometrical axes perpendicular to each other as shown in figure. Find the magnitude and direction of the net magnetic field produced at the point O.
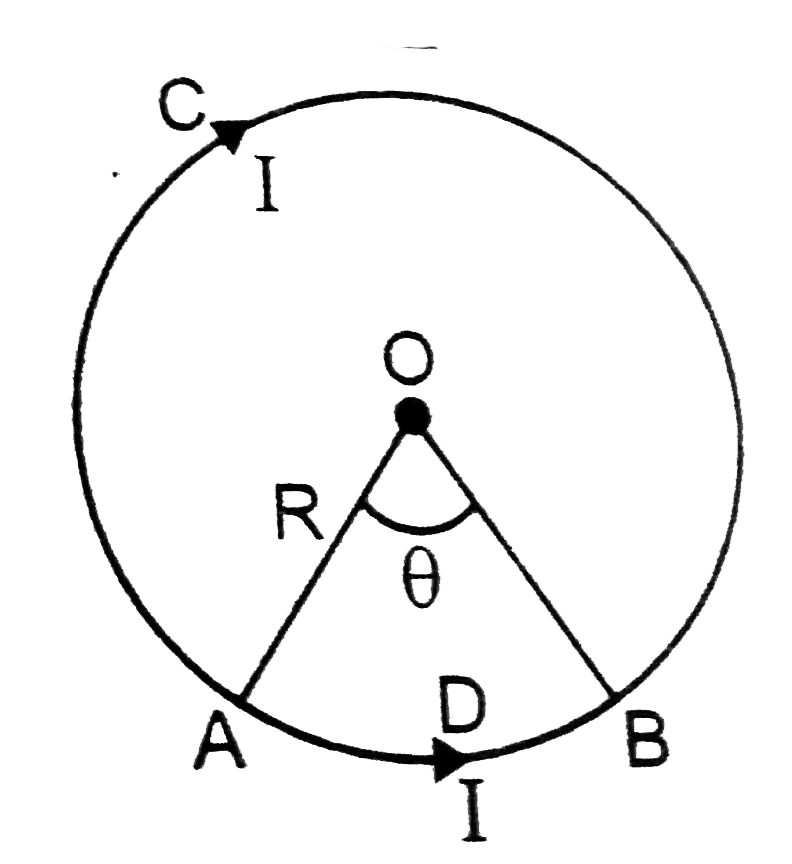
View SolutionEqual current I flows in two segments of a circular loop in the direction shown in figure. Radius of loop is R. What is the magnitude of magnetic field induciton at the centre of the loop?
View SolutionA current - carrying loop is shown in the figure. The magnitude of the magnetic field produced at a point O is
View SolutionTwo small homogeneous circular loops with traces (1) and (2), in which the same currents are flowing, are placed such that their geometric axes are perpendicular to each other as shown in the figure. Find the magnitude and direction of the net magnetic field at point O.
View SolutionA current circular conducting loop exerts a magnetic field both inside and outside it. The magnetic field at the cetre of a current loop of radius 'R' and carrying a current I is given as :
B=μ0I2R
The magnetic field lines due to a circular current loop form closed loops. The direction of the magnetic field is given by the right hand thumb rule, which states that if one curls the palm of his right hand around the current loop with the fingers pointing in the direction of the current, the right hand thumb will give the direction of the magnetic field. From this law it is clear that the direction of magnetic field →B is always perpendicular to the direction of flow of current or perpendicular to the plane of circular current loop.
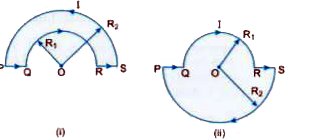
Determine the magnetic field at the centre point O due to two concentric semicircular loops of radii R1andR2 carrying a current I, when the loops of radii R1andR2 carrying a current I, when the loops are arranged as shown in Fig.
View SolutionTwo small identical circular loops, marked (1) and (2), carrying equal currents are placed with the geometrical axes perpendicular to each other as shown in the fig. Find the fig. Find the magnitude and direction of the net magnetic field at the net magnetic field at the point O.
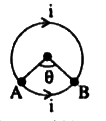
View SolutionEqual current 'i' flows in the two segments of a circular loop in the direction shown in fig. radius fo the loop is 'a'. Magnetic field at the centre of the loop is
View SolutionThe magnetic field at the centre of a current -carrying circular loop is …….to the current and ……to the loop.s radius .
View SolutionA circular loop of radius 9.7 cm carries a current 2.3A. Obtain the magnitude of the magnetic field:- centre of the loop .
View SolutionEqual current I flows in two segments of a circular loop in the direction shown in figure. Radius of loop is R. What is the magnitude of magnetic field induciton at the centre of the loop?
View Solution
