Two small identical circular loops, marked (1) and (2), carrying equal currents are placed with the geometrical axes perpendicular to each other as shown in the fig. Find the fig. Find the magnitude and direction of the net magnetic field at the net magnetic field at the point O.
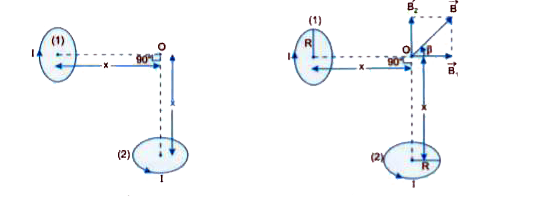
We know that the magnetic field at a point on the axial line of a small current loop of radius R is given by
B=μ0IR22x3
∴ Magnetic field at point O due to current loop number 1
B1=μ0IR22x3 along + ve X - axis.
and magnetic field at point O due to current loop number 2
B2=μ0IR22x3 along + ve Y-axis
As B1andB2 are in mutually perpendicular directions (fig.) , the resulatant magnetic field subtends an angle B from horizontal, where
tanβ=B2B1=1⇒β=45∘
Topper's Solved these Questions
- MOVING CHARGES AND MAGNETISM BOOK - U-LIKE SERIESCHAPTER - MOVING CHARGES AND MAGNETISM EXERCISE - LONG ANSWER QUESTIONS-II
11 Videos
- MOVING CHARGES AND MAGNETISM BOOK - U-LIKE SERIESCHAPTER - MOVING CHARGES AND MAGNETISM EXERCISE - SELF ASSESSMENT TEST (SECTION A) (MULTIPLE CHOICE QUESTIONS)
5 Videos
- MOVING CHARGES AND MAGNETISM BOOK - U-LIKE SERIESCHAPTER - MOVING CHARGES AND MAGNETISM EXERCISE - SHORT ANSWER QUESTIONS
41 Videos
- MODEL TEST PAPER 3 (UNSOLVED)BOOK - U-LIKE SERIESCHAPTER - MODEL TEST PAPER 3 (UNSOLVED)EXERCISE - SECTION A
3 Videos
- NUCLEIBOOK - U-LIKE SERIESCHAPTER - NUCLEIEXERCISE - Self Assessment Test
10 Videos
Similar Questions
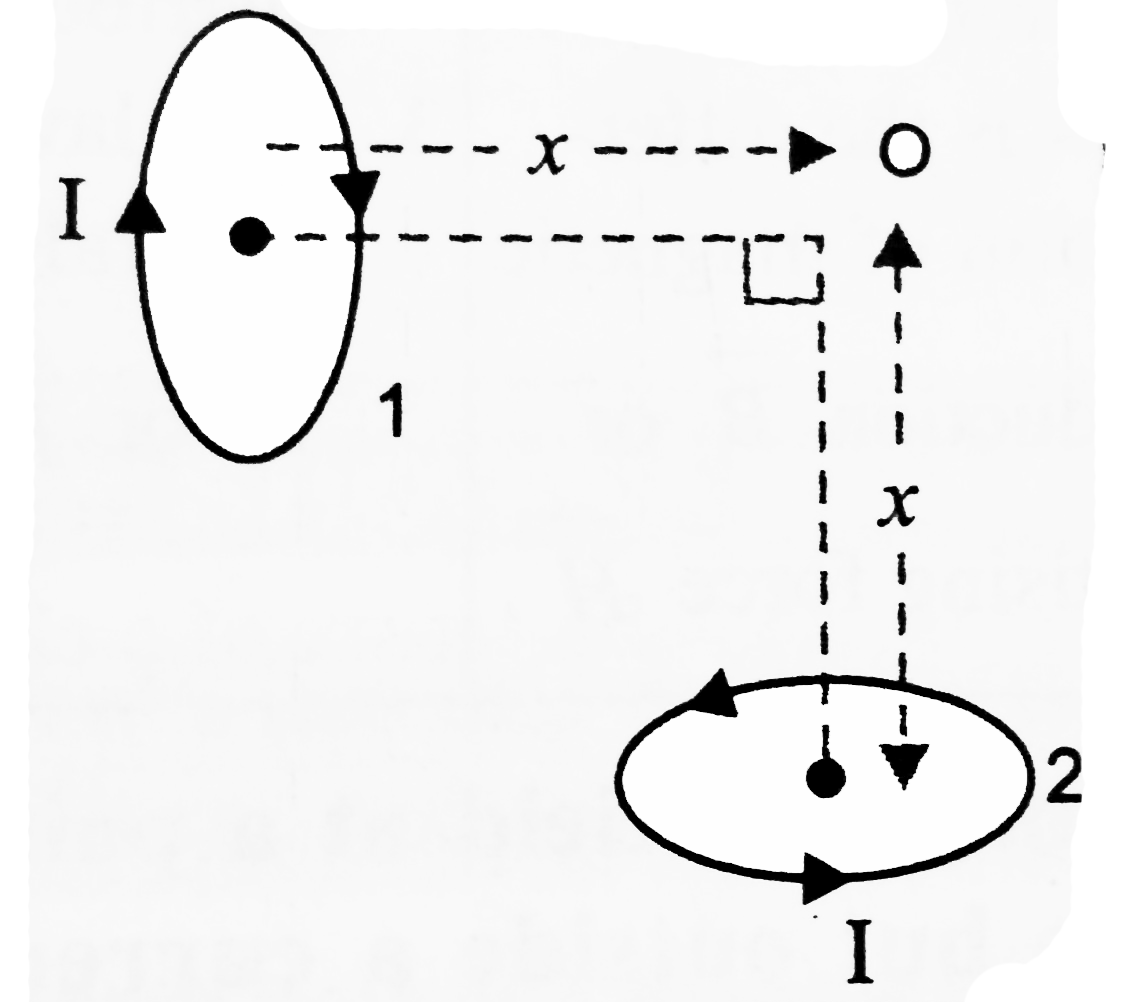
Two small circular loops, marked (1) and (2), carrying equal currents are placed with the geometrical axes perpendicular to each other as shown in figure. Find the magnitude and direction of the net magnetic field produced at the point O.
View SolutionTwo very small identical circular loops (1)and(2) carrying equal currents I are placed vertically (w.r.t. the plane of the paper) with their geometrical axes perpendicualr to each other as shown in figure. Find the magnitude and direction of the net magnetic field produced at point O.
View Solution(a) Using Biot-Savart's law, derive an expression for the magnetic field at the centre of a circular coil of radius R, number of turns N, carrying current.
(b) Two small identical circular coils marked 1,2 carry equal currents and are placed with their geometric axes perpendicular to each other as shown in the figure. Derive an expression for the resultant magnetic field at O.

View Solution(a) Using Biot-Savart's law, derive an expression for the magnetic field at the centre of a circular coil of radius R, number of turns N, carrying current.
(b) Two small identical circular coils marked 1,2 carry equal currents and are placed with their geometric axes perpendicular to each other as shown in the figure. Derive an expression for the resultant magnetic field at O.

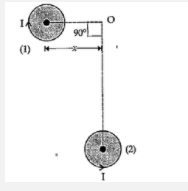
View SolutionTwo identical circular coils, P and Q, carrying currents 1A and √3A respectively, are placed concentrically and perpendicular to each other lying in the XY and YZ plane. Find the magnitude and direction of the net magnetic field at the centre of the coils.
View SolutionTwo identical circular coils, P and Q each of radius R, carrying currents 1 A and √3 A respectively, are placed concentrically are perpendicualr to each other lying in the XY and YZ planes. Find the magnitude and direction of the net magnetic field at the centre of the coils.

View SolutionTwo identical circular loops P and Q carrying equal currents are placed such that their geometrical axis are perpendicular to each other as shown in figure. And the direction of current appear’s anticlockwise as seen from point O which is equidistant from loop P and Q. Find the magnitude and direction of the net magnetic field produced at the p oint O.
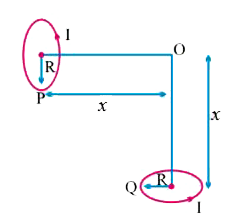
tanθ=B2B1=1,θ=π/4.
View SolutionFind the magnitude and direction of magnetic field at point P due to the current carrying wire as shown in

View SolutionFind the magnitude and direction of magnetic field at point P due to the current carrying wire as shown in

View SolutionFig shows two current-carrying wires 1 and 2. Find the magnitudes and directions of the magnetic field at points P,Q and R.

View Solution
