Determine the force between two parallel circular coaxial coils of radius R each, which are a small distance d(d<<R) apart in free space and carry indentical currents I. Assume that each of the coils has a single turn.
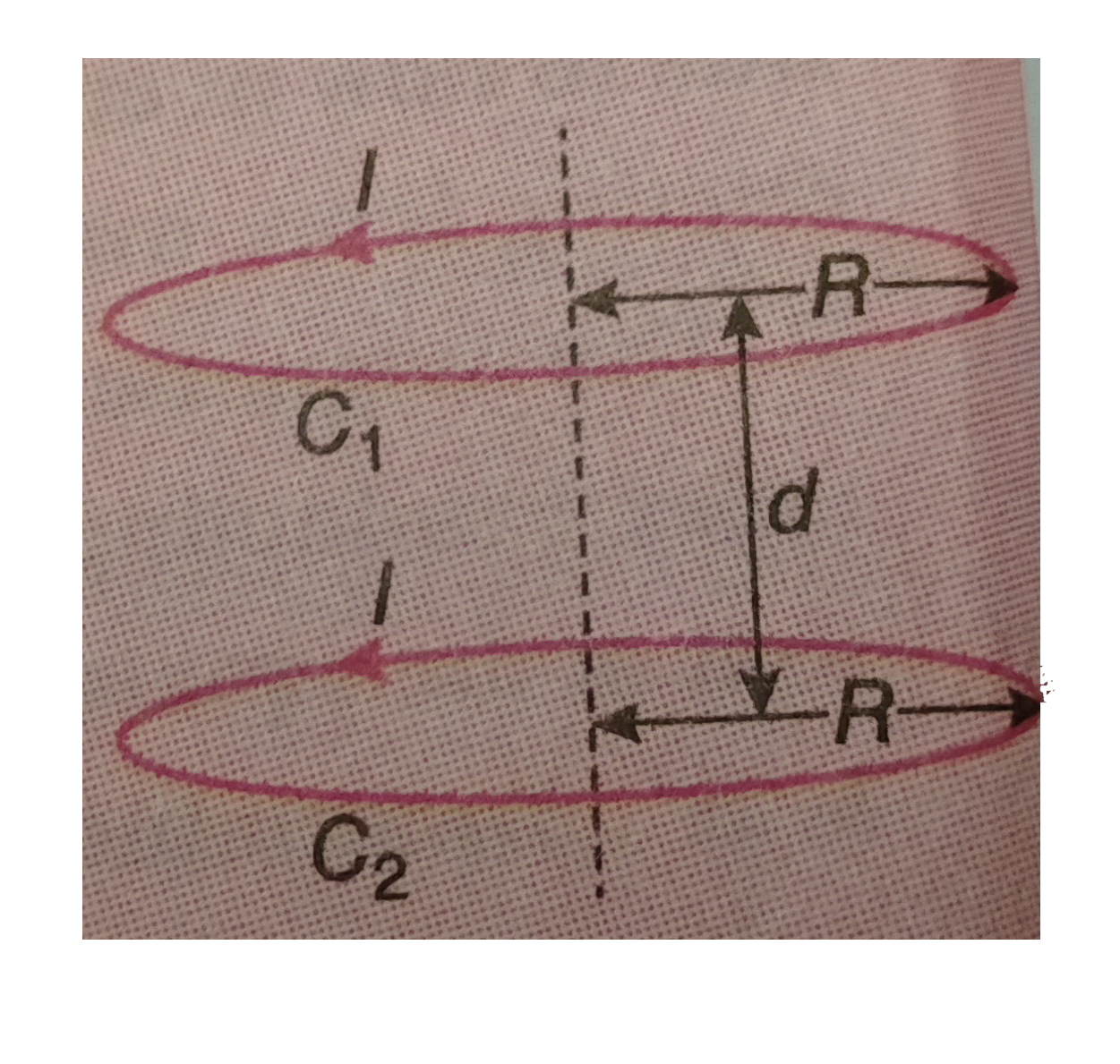
Let the two coils be denoted by C1andC2. As d is much smaller than the radius (R) or each soil, the force per unit length on one of the coils (say C1) due to the other coil (C2) can be approximated as
F0=μ02πd(I)(I)
The net force on C1 is F=πRF0=μ0(I)(I)Rd=μ0I2Rd
The two coils will attract each other with this force if I for both are in same direction.
Topper's Solved these Questions
- ELECTROMAGNETISM BOOK - CHHAYA PUBLICATIONCHAPTER - ELECTROMAGNETISM EXERCISE - NCERT TEXTBOOK QUESTIONS WITH ANSWER HINT
25 Videos
- ELECTROMAGNETISM BOOK - CHHAYA PUBLICATIONCHAPTER - ELECTROMAGNETISM EXERCISE - NCERT EXAMPLAR QUESTIONS WITH ANSWER HINT (MCQ-1)
2 Videos
- ELECTROMAGNETISM BOOK - CHHAYA PUBLICATIONCHAPTER - ELECTROMAGNETISM EXERCISE - SECTION RELATED QUESTIONS
64 Videos
- ELECTROMAGNETIC WAVES BOOK - CHHAYA PUBLICATIONCHAPTER - ELECTROMAGNETIC WAVES EXERCISE - CBSE SCANNER
17 Videos
- ELEMENTARY PHENOMENA OF ELECTROSTATICS BOOK - CHHAYA PUBLICATIONCHAPTER - ELEMENTARY PHENOMENA OF ELECTROSTATICS EXERCISE - EXAMINATION ARCHIVE
2 Videos
Similar Questions
Find the force between two small circular coils of radii r1=1cm,r2=2cm and currents I1=1A and I2=2A placed at d=20cm apart with their planes parallel to each other.
View SolutionTwo identical current carrying coils of radius 10 cm each are placed coaxially0.5 m apart. Find the magnetic fields at the centre of each coil if a current of 0.5 A is passed through each of them in opposite directions. Assume that each coil is made of a single turn.
View Solution
Knowledge Check
A circular current-carrying coil has a radius R. The distance from the centre of the coil, on the axis, where B will be 1/8 of its value at the centre of the coil is
AR√3B√3RC2√3RD2R√3Two identical coils each of radius R and each carrying a current I in the same direction are placed along a common axis and separated by distance R. At the midpoint between the two coils the
Amagnetic field is zeroBmagnetic field is 0.8 sqrt(0.8)mu""_0I/RCsecond derivative of magnetic fieldDfirst derivative of magnetic field dB/dx=0Two identical coils each of radius R and each carrying a current I in the same direction are placed along a common axis and separated by distance R. At the midpoint between the two coils the
Amagnetic field is zeroBmagnetic field is 0.8 sqrt(0.8)mu""_0I/RCsecond derivative of magnetic fieldDfirst derivative of magnetic field dB/dx=0
A circular coil of wire of radius 'r' has 'n' turns and carries a current 'I'. The magnetic induction (B) at a point on the axis of the coil at a distance √3r from its centre is
View SolutionA circular coil of n turns and radius r carries a current I. The magnetic field at the centre is
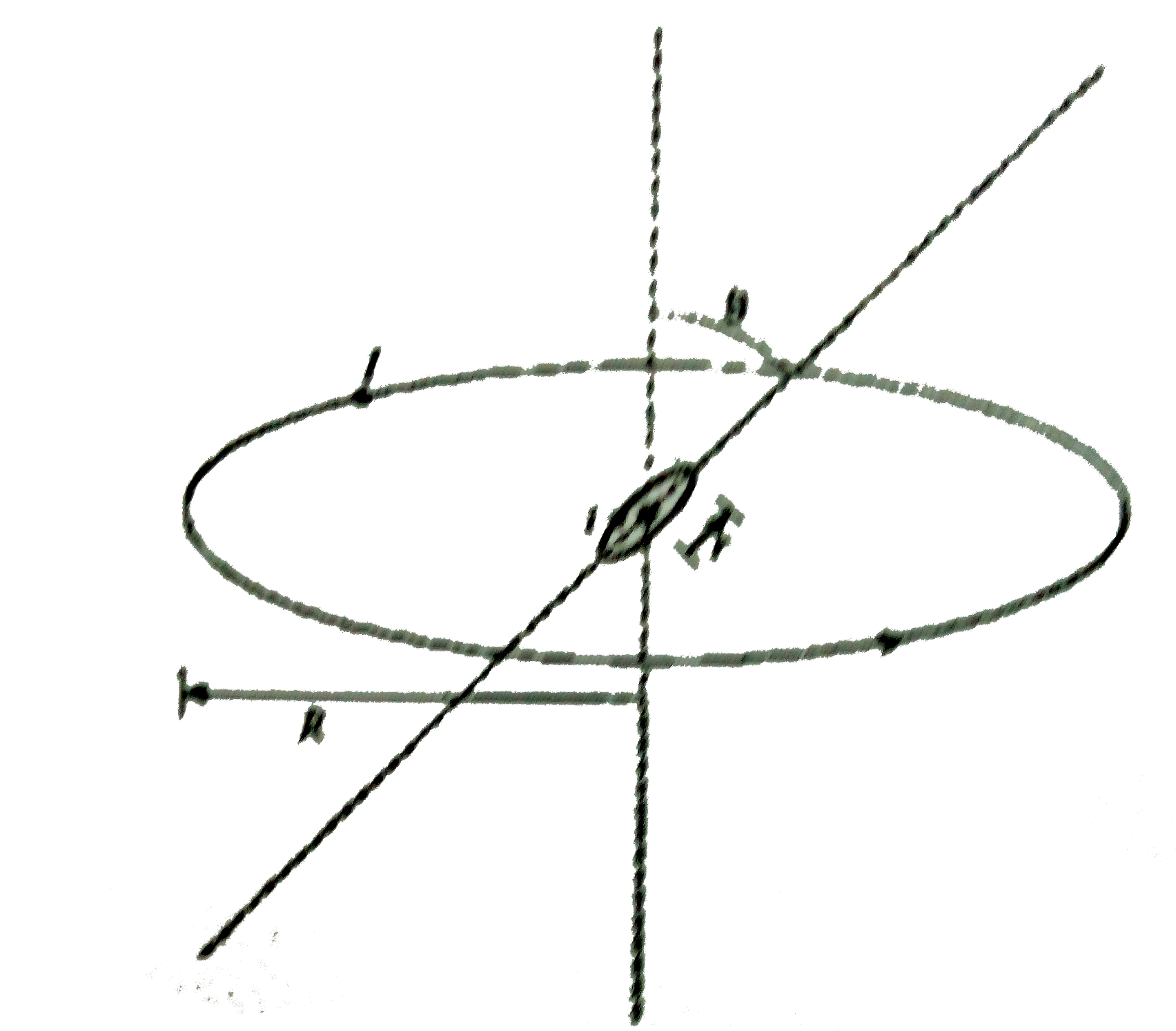
View SolutionFigure shows a larger horizontal coil of radius R carrying a current I. Another small coil of radius r(r<<R) carrying a current i & N turns is placed at the centre with its plane at an angle θ from the axis. Find the torque experienced by the smaller coil in this situation.
View SolutionA circular coil of n turns and radius r carries a current I. The magnetic field at the center is
View SolutionThe magnetic moment of a current I carrying circular coil of radius r and number of turns N varies as
View Solution
