When we jump out of a boat standing in water it moves
Forward
Backward
Sideways
None of the above
The correct Answer is:B
Step by step video, text & image solution for When we jump out of a boat standing in water it moves by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Topper's Solved these Questions
- BOOK - ERRORLESS CHAPTER - NEWTONS LAWS OF MOTIONEXERCISE - Conservation of Linear Momentum and Impulse27videos
NEWTONS LAWS OF MOTION
- BOOK - ERRORLESS CHAPTER - NEWTONS LAWS OF MOTIONEXERCISE - Equilibrium of Force18videos
NEWTONS LAWS OF MOTION
- BOOK - ERRORLESS CHAPTER - NEWTONS LAWS OF MOTIONEXERCISE - Second Law of Motion113videos
NEWTONS LAWS OF MOTION
- BOOK - ERRORLESS CHAPTER - MOTION IN TWO DIMENSIONEXERCISE - Exercise319videos
MOTION IN TWO DIMENSION
- BOOK - ERRORLESS CHAPTER - ROTATIONAL MOTIONEXERCISE - Practice Problems (Problems based on motion of connected mass)10videos
ROTATIONAL MOTION
Similar Questions
Knowledge Check
- Question 1 - Select One
When we jump out of a boat standing in water it moves
ABackwardBForwardCSidewaysDNoneof these - Question 2 - Select One
When the speed of a boat in still water is 4 km/h and the rate of stream is 2 km/h, find upstream speed of the boat
A6 km/hB5 km/hC2 km/hD7 km/h - Question 3 - Select One
A boat goes 40 km upstream in 8 hours and 36 km downstream in 6 hours. The speed of the boat in still water is
A6.5 km/hrB6 km/hrC5.5 km/hrD5 km/hr
This summer we had gone to USA for a fun trip. For a change, we decided to take a motor boat along Niagra river. I hand heard a lot about Niagra water falls is 50 m high. What an adventure it would be to fall freely with the water fall. We started about 20 km upstream of the watyer fall with a motor boat which could travel at 18 km/hr relative to the water. the Biagra river is a slowly flowing river, flowing at pleasant 3.6 km/hr. The river is almost 300 m wide and we decided to go downstream with engine of motor boat on. Hardly we had gone 3-4 km when we noticed a long tree of length almost 10 m flowing 50 m away from us. our line of motion was passing through the centre of the tree which was oriented perpendicular to river flows. sensing our uneasiness, the boatman took a left turn by an angle θ (as seen by us) and we just managed to cross the tree. thereafter, the boat moved only downstreas as before. as we reached Niagra falls. the velocity of boat and the river was horizontal. the boat flew in the air and struck the water below at an angle to the horizontal. vow! That an experience of life.
What was the distance between point of impact of boat and falling water ?View SolutionWe know that when a boat travels in water, its net velocity w.r.t. ground is the vector sum of two velocities. First is the velocity of boat itself in river and other is the velocity of water w.r.t. ground. Mathematically:

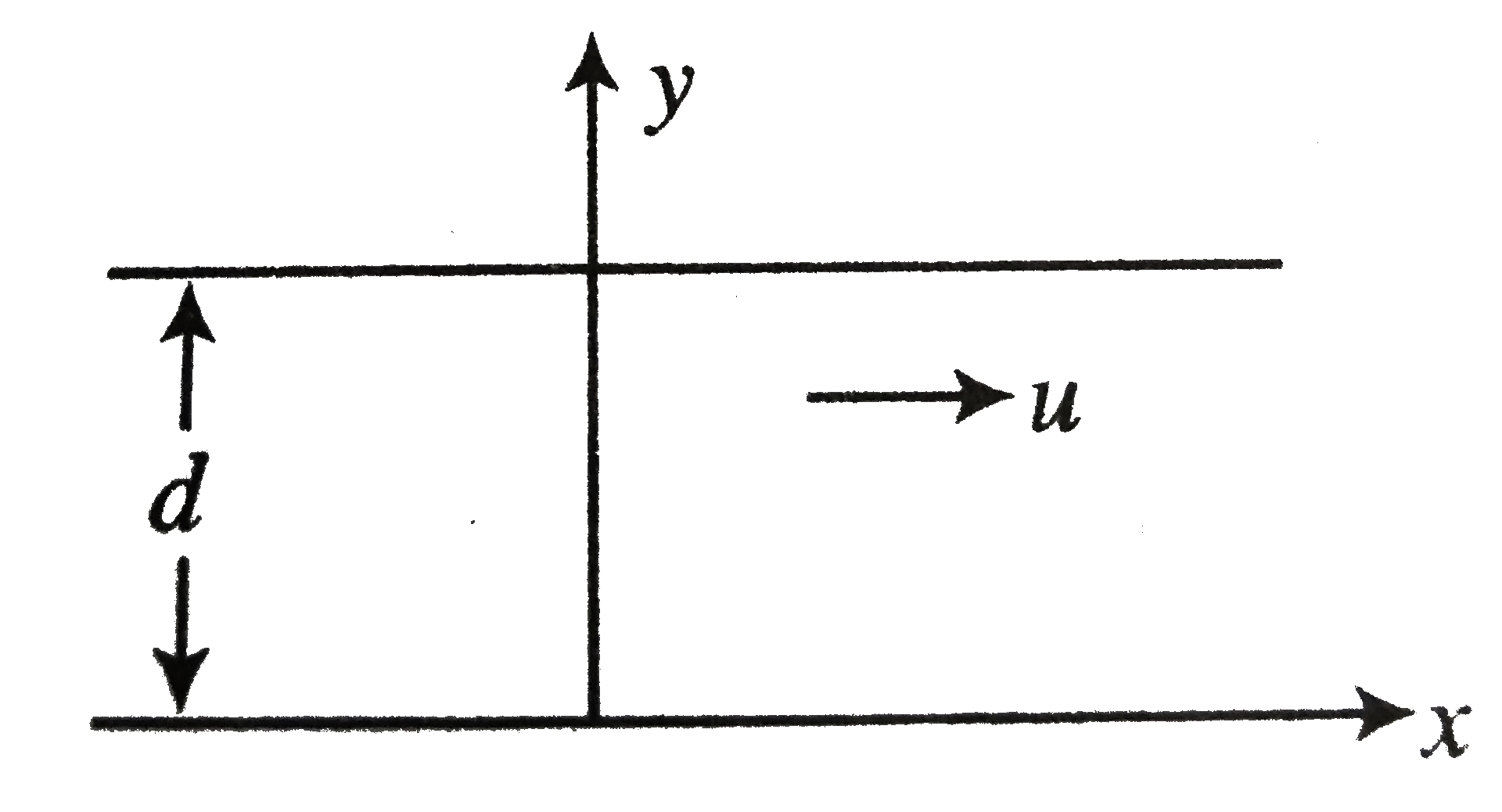
→vboat=→vboat,water+→vwater.
Now given that velocity of water w.r.t. ground in a river is u. Width of the river is d.
A boat starting from rest aims perpendicular to the river with an acceleration of a = 5t, where t is time. The boat starts from point (1,0) of the coordinate system as shown in figure. Assume SI units.View SolutionWe know that when a boat travels in water, its net velocity w.r.t. ground is the vector sum of two velocities. First is the velocity of boat itself in river and other is the velocity of water w.r.t. ground. Mathematically:
→vboat=→vboat,water+→vwater.
Now given that velocity of water w.r.t. ground in a river is u. Width of the river is d.
A boat starting from rest aims perpendicular to the river with an acceleration of a = 5t, where t is time. The boat starts from point (1,0) of the coordinate system as shown in figure. Assume SI units.View SolutionWe know that when a boat travels in water, its net velocity w.r.t. ground is the vector sum of two velocities. First is the velocity of boat itself in river and other is the velocity of water w.r.t. ground. Mathematically:
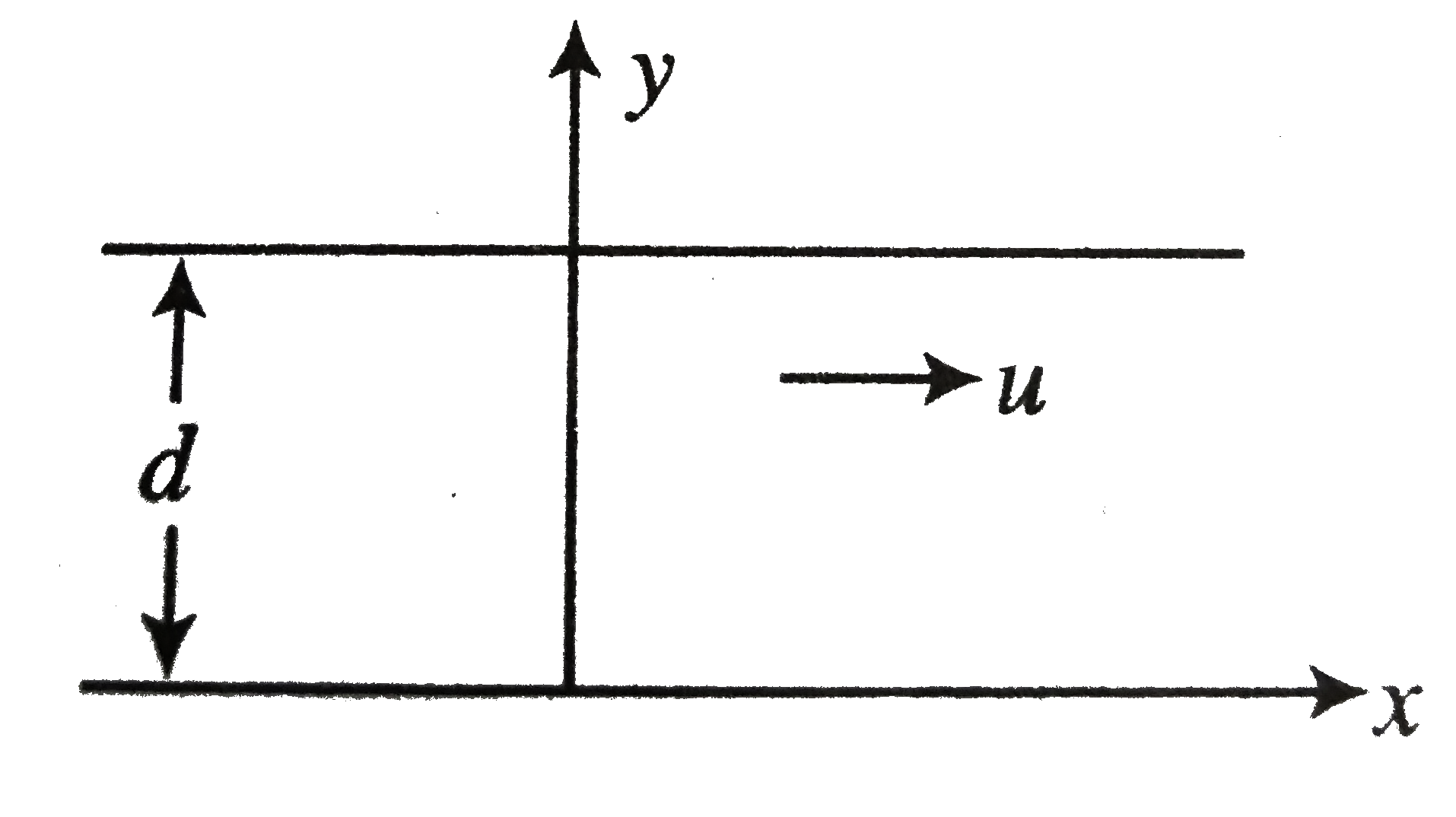
→vboat=→vboat,water+→vwater.
Now given that velocity of water w.r.t. ground in a river is u. Width of the river is d.
A boat starting from rest aims perpendicular to the river with an acceleration of a = 5t, where t is time. The boat starts from point (1,0) of the coordinate system as shown in figure. Assume SI units.View SolutionA man stands at one end of a boat which is stationary in water. Neglect water resistance. The man now moves to the other end of the boat and again becomes stationary. The centre of mass of the man plus boat system will remain stationary with respect to water.
View Solution

