Read the following passage carefully and answer the questions
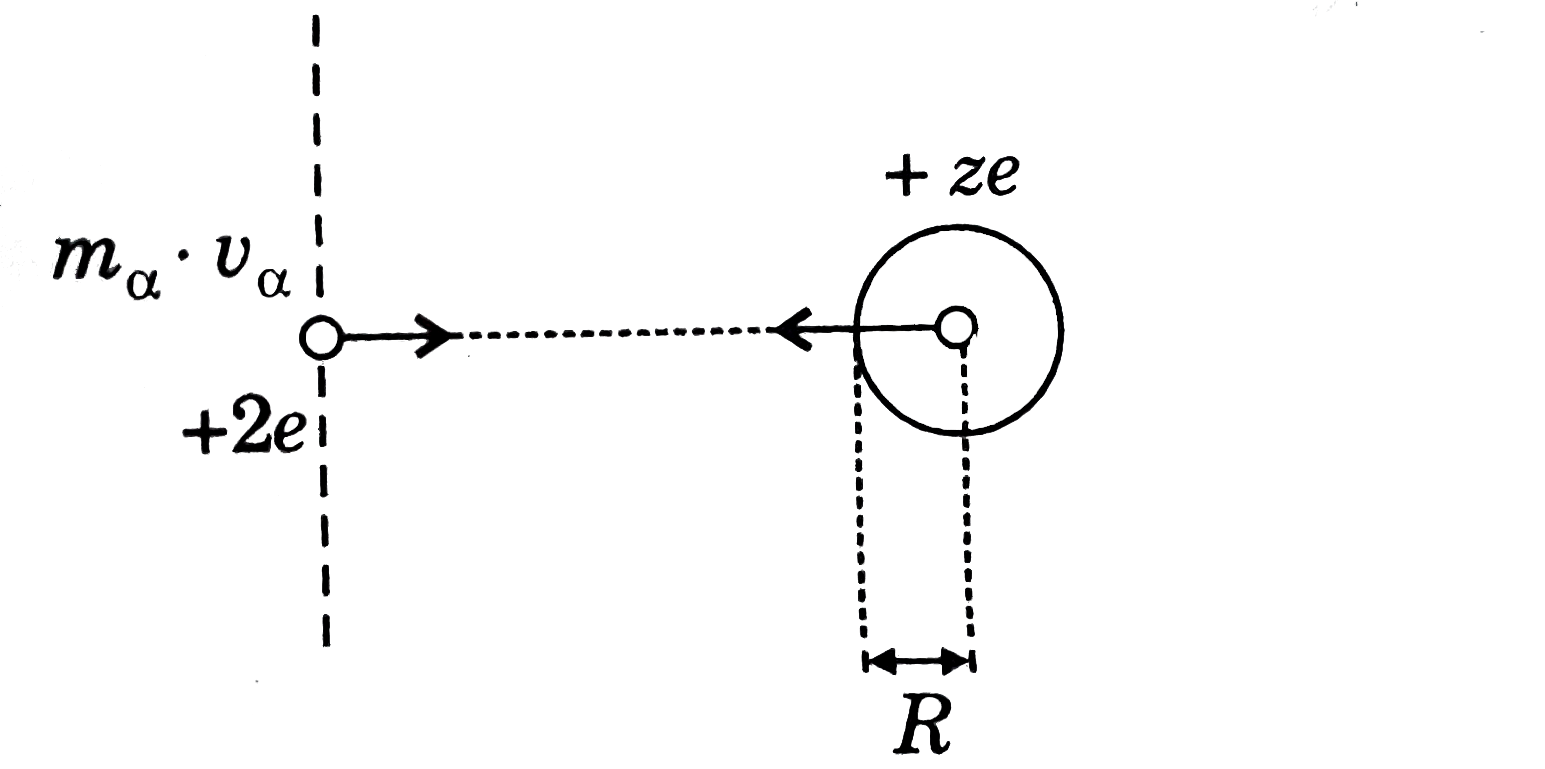
The approximate size of the nucleus can be calculated by using energy conservation theorem in Rutherford's α−scattering experiment. If an α−perticle is projected from infinity with speed v, towards the nucleus having z protons then the apha−perticle which is reflected back or which is deflected by 180∘ must have approach closest to the nucleus. It can be approximated that α−particles collides with the nucleus and gets back. Now if we apply the energy conservation at initial and collision point then:
(Total Energy)initial=(Total Enregy)final
(KE)i+(PE)i=(KE)f+(PE)f
(PE)i=0,sincePE of two charge system separated by infinite distance is zero, finally the particle stops and then starts coming back.
12mαv2α+0=0+kq1q2R
⇒12mαv2α=k2e×zeR⇒R=4kze2mαv2α
Thus the radius of nucleus can be calculated using above equation. The nucleus is so small a particle that we can't define a sharp boundary for it . Experiments show that the average radius R fo a nucleus may be written as
R=R0(A)1/3
where R0=1.2×10−15m
A= atomic mass number
R=radius of nucleus
Radius of a particular nucleus is calculated by the projection of α−particle from infinity at a particular speed. Let this radius be the true radius. If the radius calculation for the same nucleus is made by , α−particle with half of the earlier speed then the percentage error involved in the radius calculation is :
0.75
1
3
4
The correct Answer is:c
Step by step video, text & image solution for Read the following passage carefully and answer the questions The approximate size of the nucleus can be calculated by using energy conservation theorem in Rutherford's alpha-scattering experiment. If an alpha-perticle is projected from infinity with speed v, towards the nucleus having z protons then the apha-perticle which is reflected back or which is deflected by 180^(@) must have approach closest to the nucleus. It can be approximated that alpha-particles collides with the nucleus and gets back. Now if we apply the energy conservation at initial and collision point then: ("Total Energy")_("initial") = ("Total Enregy")_("final") (KE)_(i) +(PE)_(i)=(KE)_(f)+(PE)_(f) (PE)_(i) =0, "since"PE of two charge system separated by infinite distance is zero, finally the particle stops and then starts coming back. 1/2m_(alpha)v_(alpha)^(2) + 0=0 + (kq_(1)q_(2))/(R) rArr1/2m_(alpha)v_(alpha)^(2)=k(2exxze)/(R)rArrR=(4kze^(2))/(m_(alpha)v_(alpha)^(2) Thus the radius of nucleus can be calculated using above equation. The nucleus is so small a particle that we can't define a sharp boundary for it . Experiments show that the average radius R fo a nucleus may be written as R=R_(0)(A)^(1//3) where R_(0) = 1.2xx10^(-15)m A= atomic mass number R=radius of nucleus Radius of a particular nucleus is calculated by the projection of alpha-particle from infinity at a particular speed. Let this radius be the true radius. If the radius calculation for the same nucleus is made by , alpha-particle with half of the earlier speed then the percentage error involved in the radius calculation is : by Chemistry experts to help you in doubts & scoring excellent marks in Class 11 exams.
Topper's Solved these Questions
- BOOK - GRB PUBLICATIONCHAPTER - ATOMIC STRUCTUREEXERCISE - Match the column type16videos
ATOMIC STRUCTURE
- BOOK - GRB PUBLICATIONCHAPTER - ATOMIC STRUCTUREEXERCISE - Subjective Type55videos
ATOMIC STRUCTURE
- BOOK - GRB PUBLICATIONCHAPTER - ATOMIC STRUCTUREEXERCISE - Multiple Objective Type49videos
ATOMIC STRUCTURE
- BOOK - GRB PUBLICATIONCHAPTER - CHEMICAL EQUILIBRIUMEXERCISE - D.Le Chateliera principle16videos
CHEMICAL EQUILIBRIUM
Similar Questions
Rutherford model: The approximate size of the nucleus can be calculated by using energy conservation theorem in Rutherford's α-scattering experiment. If an α-particle is projected from infinity with speed v towards the nucleus having Z protons, then the α-particle which is reflected back or which is deflected by 180∘ must have approached closest to the nucleus .It can be approximated that α particle collides with the nucleus and gets back. Now if we apply the energy conservation equation at initial point and collision point then:
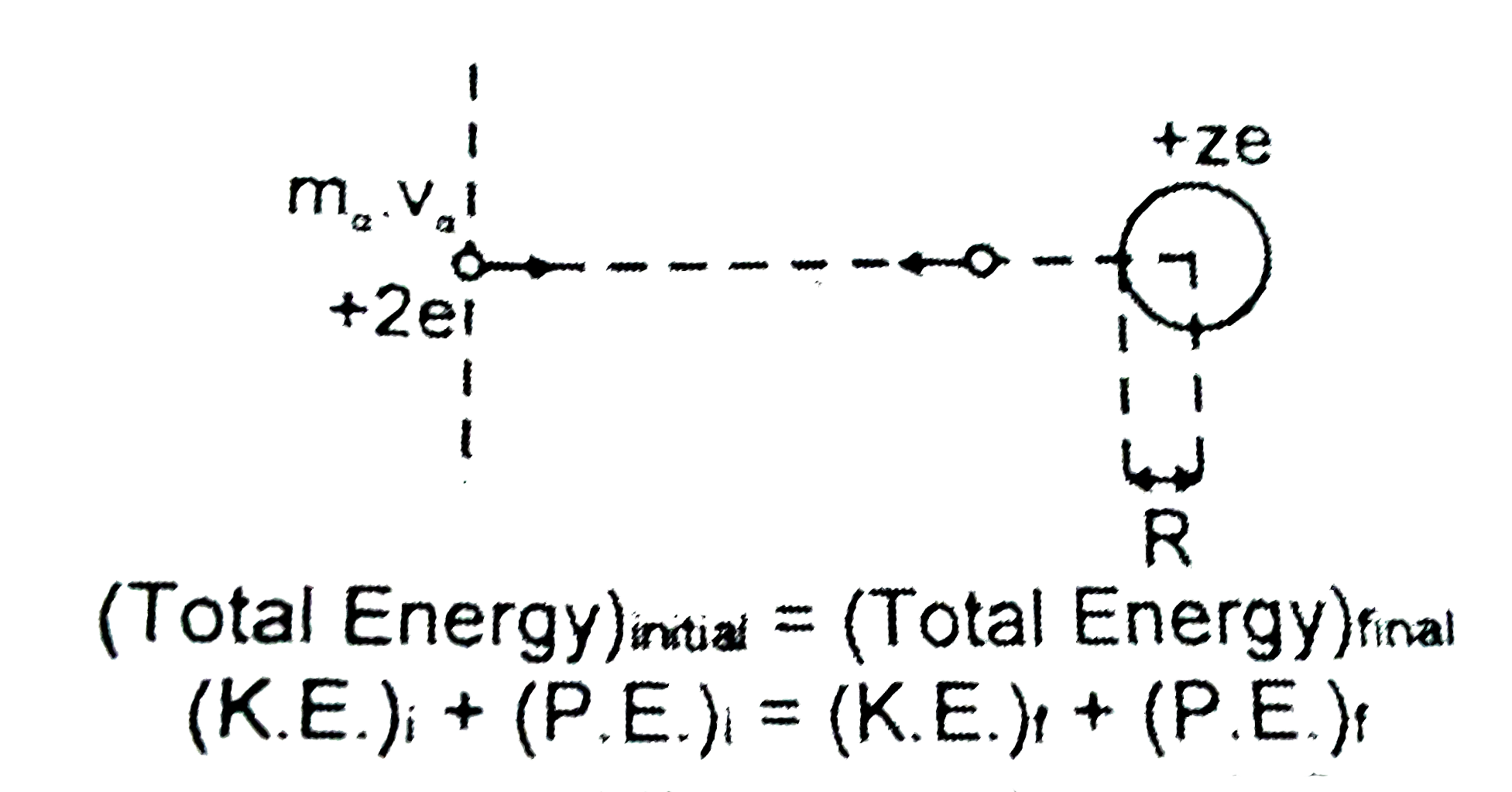
(P.E.)i=0, since P.E. of two charge system separated by infinite distance is zero. Finally the particle stops and then starts coming back.
12mαv2α+0=0+Kq1q2R⇒12mαv2α=K2e×ZeR⇒R=4KZe2mαv2α
Thus the radius of nucleus can be calculated using above equation. The nucleus is so small a particle that we can't define a sharp boundary for it
An α-particle with initial speed v0 is projected from infinity and it approaches up to r0 distance from a nuclie. Then, the initial speed of α-particle, which approaches upto 2r0 distance from the nucleus is :View SolutionWhich fact is proved by the following observation in Rutherford's scattering experiment' very few alpha particles are deflected back'?
View Solution
Knowledge Check
- Question 1 - Select One
Read the following passage carefully and answer the questions
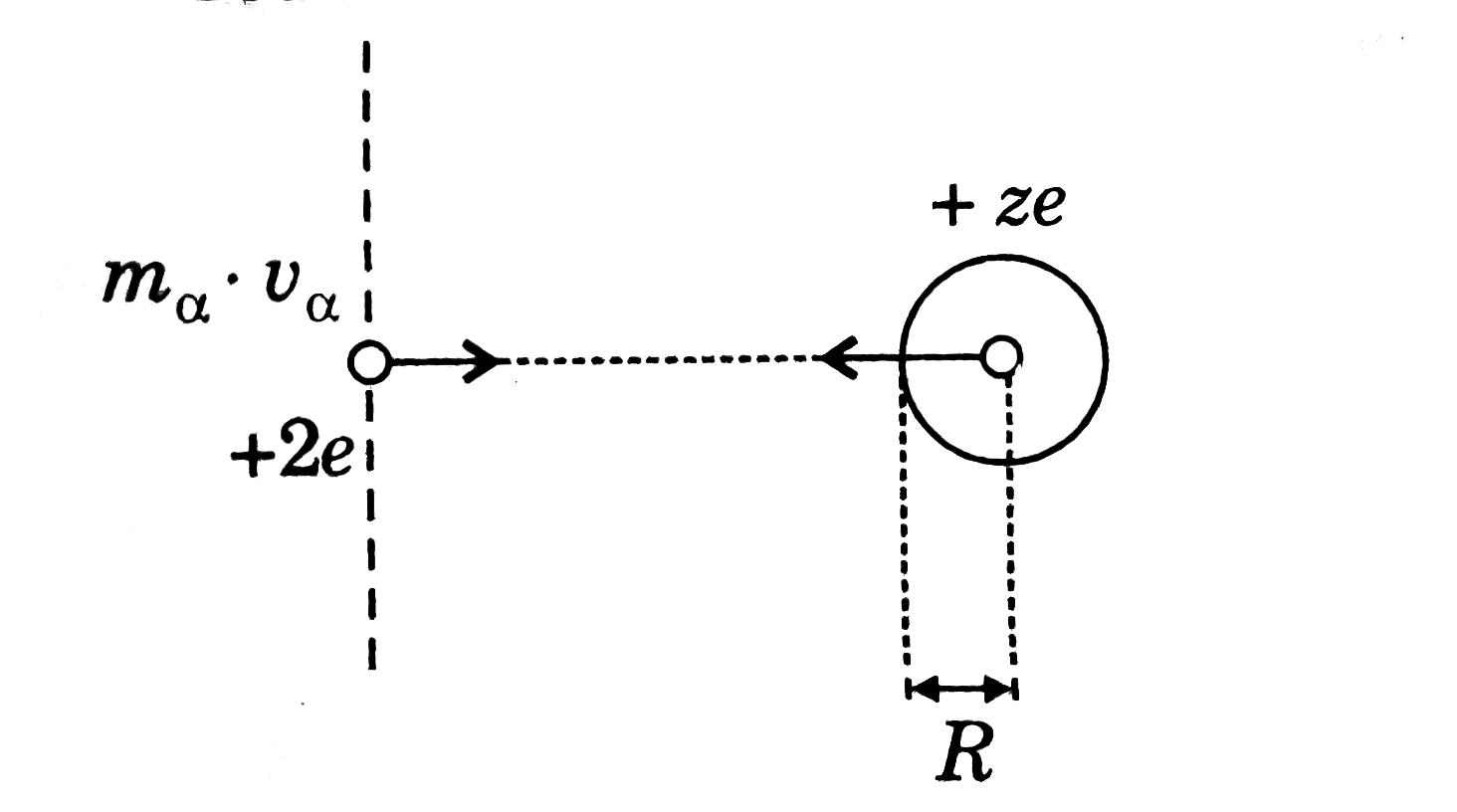
The approximate size of the nucleus can be calculated by using energy conservation theorem in Rutherford's α−scattering experiment. If an α−perticle is projected from infinity with speed v, towards the nucleus having z protons then the apha−perticle which is reflected back or which is deflected by 180∘ must have approach closest to the nucleus. It can be approximated that α−particles collides with the nucleus and gets back. Now if we apply the energy conservation at initial and collision point then:
(Total Energy)initial=(Total Enregy)final
(KE)i+(PE)i=(KE)f+(PE)f
(PE)i=0,sincePE of two charge system separated by infinite distance is zero, finally the particle stops and then starts coming back.
12mαv2α+0=0+kq1q2R
⇒12mαv2α=k2e×zeR⇒R=4kze2mαv2α
Thus the radius of nucleus can be calculated using above equation. The nucleus is so small a particle that we can't define a sharp boundary for it . Experiments show that the average radius R fo a nucleus may be written as
R=R0(A)1/3
where R0=1.2×10−15m
A= atomic mass number
R=radius of nucleus
If the diameter of two different nuclei are in the ratio 1:2 then their mass number are in the ratio:A0.043055555555556B0.33402777777778C0.047222222222222D0.044444444444444 - Question 2 - Select One
Read the following passage carefully and answer the questions
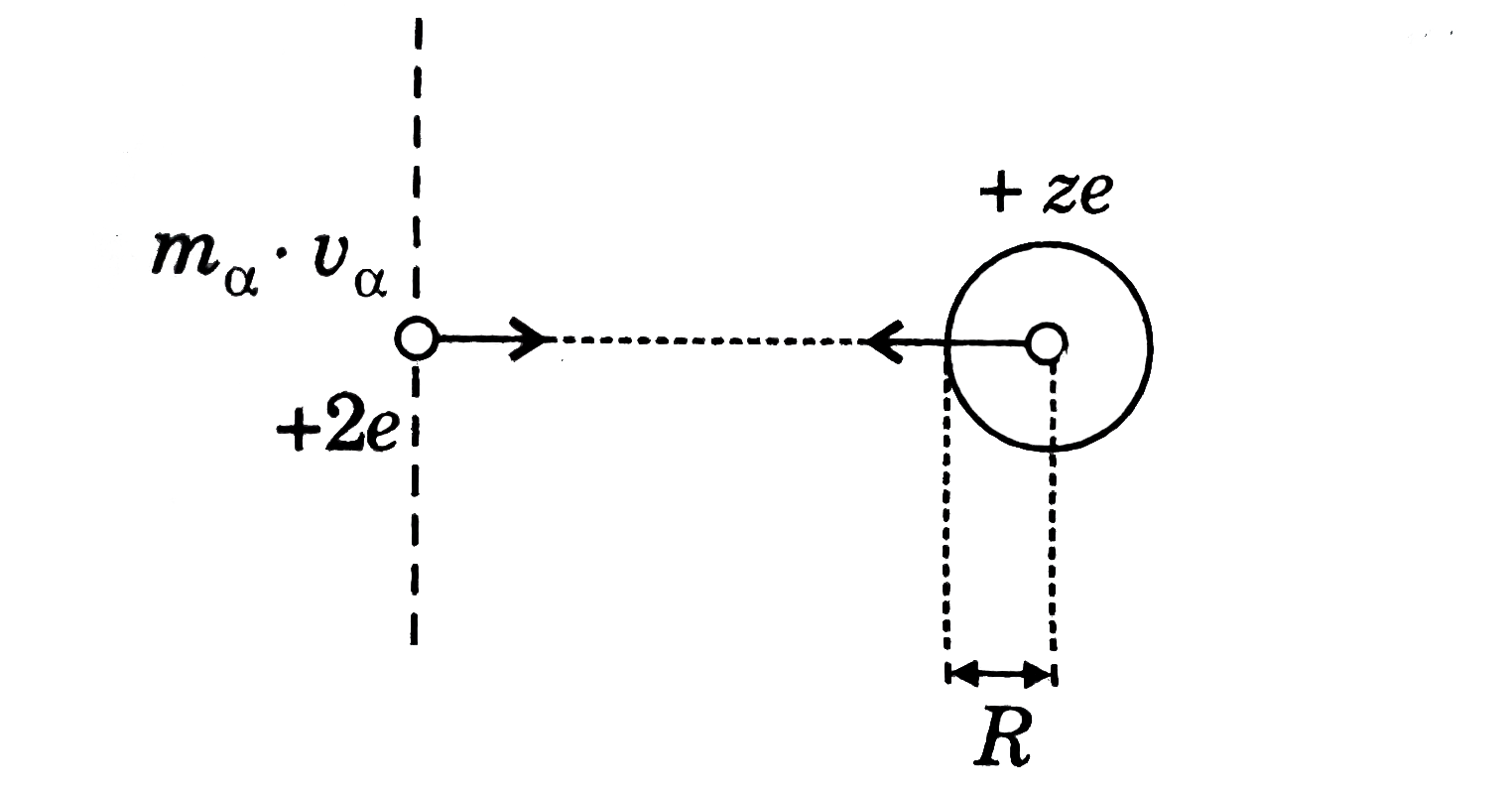
The approximate size of the nucleus can be calculated by using energy conservation theorem in Rutherford's α−scattering experiment. If an α−perticle is projected from infinity with speed v, towards the nucleus having z protons then the apha−perticle which is reflected back or which is deflected by 180∘ must have approach closest to the nucleus. It can be approximated that α−particles collides with the nucleus and gets back. Now if we apply the energy conservation at initial and collision point then:
(Total Energy)initial=(Total Enregy)final
(KE)i+(PE)i=(KE)f+(PE)f
(PE)i=0,sincePE of two charge system separated by infinite distance is zero, finally the particle stops and then starts coming back.
12mαv2α+0=0+kq1q2R
⇒12mαv2α=k2e×zeR⇒R=4kze2mαv2α
Thus the radius of nucleus can be calculated using above equation. The nucleus is so small a particle that we can't define a sharp boundary for it . Experiments show that the average radius R fo a nucleus may be written as
R=R0(A)1/3
where R0=1.2×10−15m
A= atomic mass number
R=radius of nucleus
If α−particle with speed v0 is projected from infinity and it approaches upto r0 distance from the nuclei. Then the speed of α−particle which approaches 2r0 distance from the nucleus isA√2v0Bv0√2C2v0Dv02 - Question 3 - Select One
Rutherford's α- scattering experiment related to the size of the-
AnucleusBatomCelectronDneutron
Write two conclusions which have been derived from Rutherford's α-ray scattering experiment .ll
View SolutionRutherford concluded from his α-ray scattering experiment that there exists a heavy and dense body at the centre of the nucleus .
View SolutionIn Rutherford's scattering experiment of α-particles by metallic foils, with the increase of atomic number of nucleus, the scattering angle .
View SolutionRutherford's scattering experiment is related to the________of the nucleus.
View SolutionWhich of these is true regarding an α particle with mass 'm' projected towards the nucleus with velocity 'v ?
View Solution

