Fraction of oxygen molecules (dNN) in the range Umps to Umps+fUmps whre f<<1d:
4f2√π
4√π(M2RT)1/2e−1
feπ
1
The correct Answer is:a
Topper's Solved these Questions
Similar Questions
Knowledge Check
Statement-1: Distribution pattern of speed will be more uniform for H2 as compared to O2.
Statement-2: Fraction of molecules having speed equal to Umps will be more in case H2 than O2 at same T.AStatement-I is True, Statement-II is True : Statement-II is a correct explanation for Statement-IBStatement-I is True, Statement-II is True : Statement-II is NOT a correct explanation for Statement-ICStatement-I is True, Statement-II is False.DStatement-I is False, Statement-II is True.The ratio between the three speeds, ump:uav:urms is given as
A1:1.224:1.128B1:1.128:1.224C1.224:1.128:1D1.128:1.224:1If T1,T2 and T3 are the temperatures at which the urms,uaverage,ump of oxygen gas are all equal to 1500 m/s then the correct statement is :
AT1>T2>T3BT1<T2<T3CT1=T2=T3DNone of these
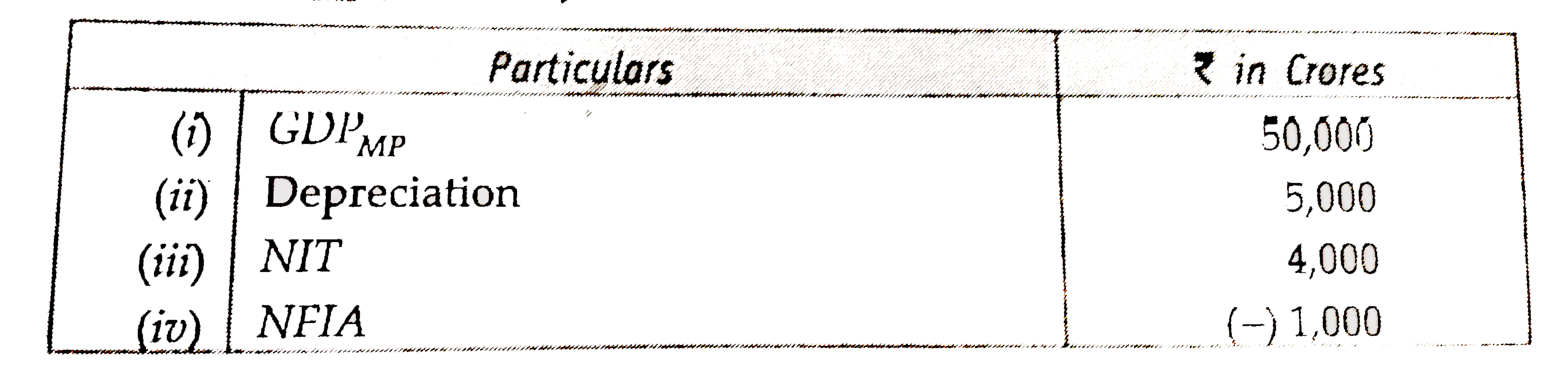
Calculate NNPMP from the following :
View SolutionIf T1,T2 and T3 are the temperatures at which the urms,uaverage,ump of oxygen gas are all equal to 1500 m/s then the correct statement is :
View SolutionThe speed of a molecule of a gas changes continuously as a result of collisions with other molecules and with the walls of the container. The speeds of individual molecules therefore change with time.
A direct consequence of the distribution of speeds is that the average kinetric energy is constant for a given temperature.
The average K.E. is defined as
¯¯¯¯¯¯KE=1N(12mΣidNiu21)=12m(ΣidNiN.u21)
where dNN is the fraction of molecules having speeds between ui and ui+du and as proposed by maxwell dNN=4π(m2πKT)3/2exp(−mu22KT).u2.du
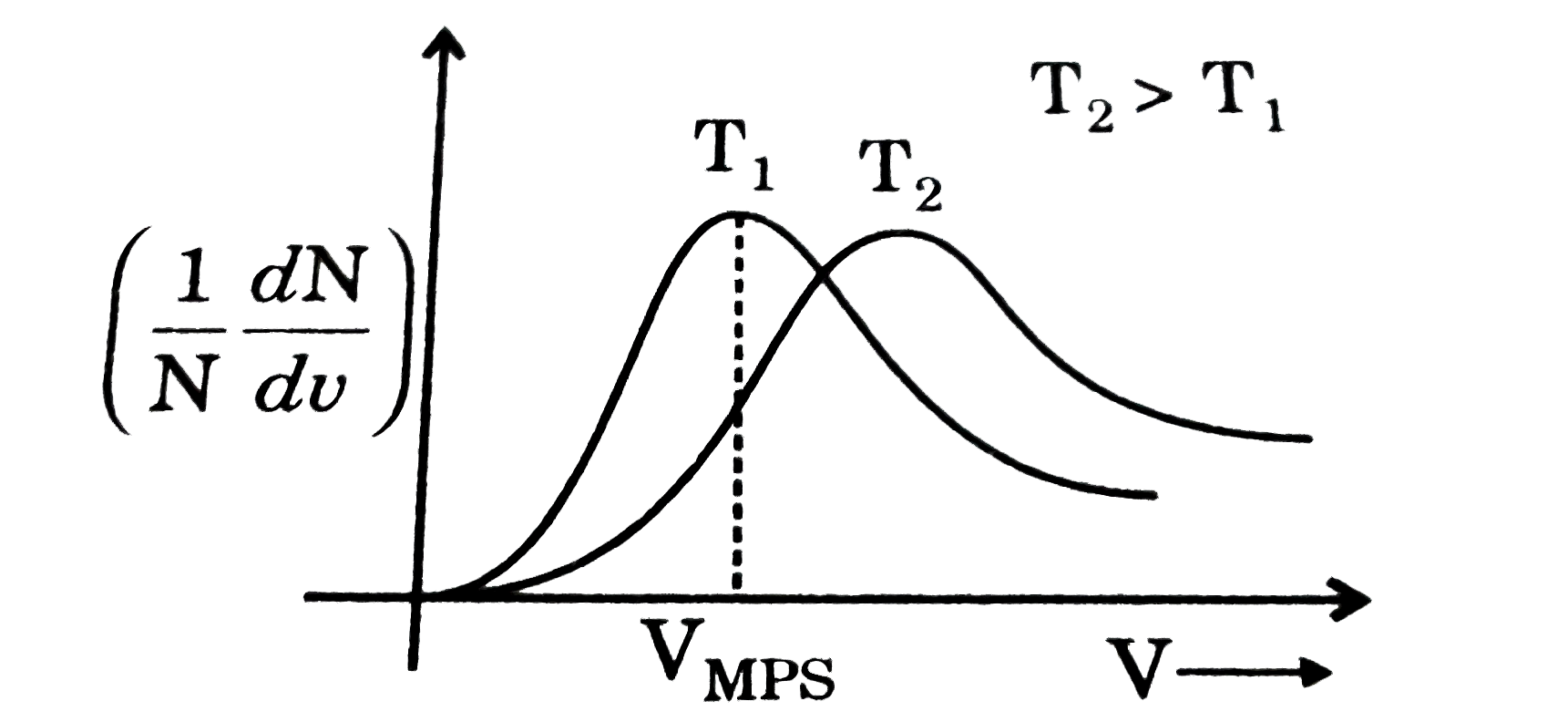
The plot of (1NdNdu) is plotted for a particular gas at two different temperature against u as shown.
The majority of molecules have speeds which cluster around vMPS in the middle of the range of v. There area under the curve between any two speeds V1andV2 is the fraction of molecules having speeds betweenV1andV2.
The speed distribution also depends on the mass of the molecules. As the area under the curve is the same (equal to unity) for all gas samples, samples which have the same VMPS will have identical Maxwellian plots. On the basis of the above passage answer the questions that follow.
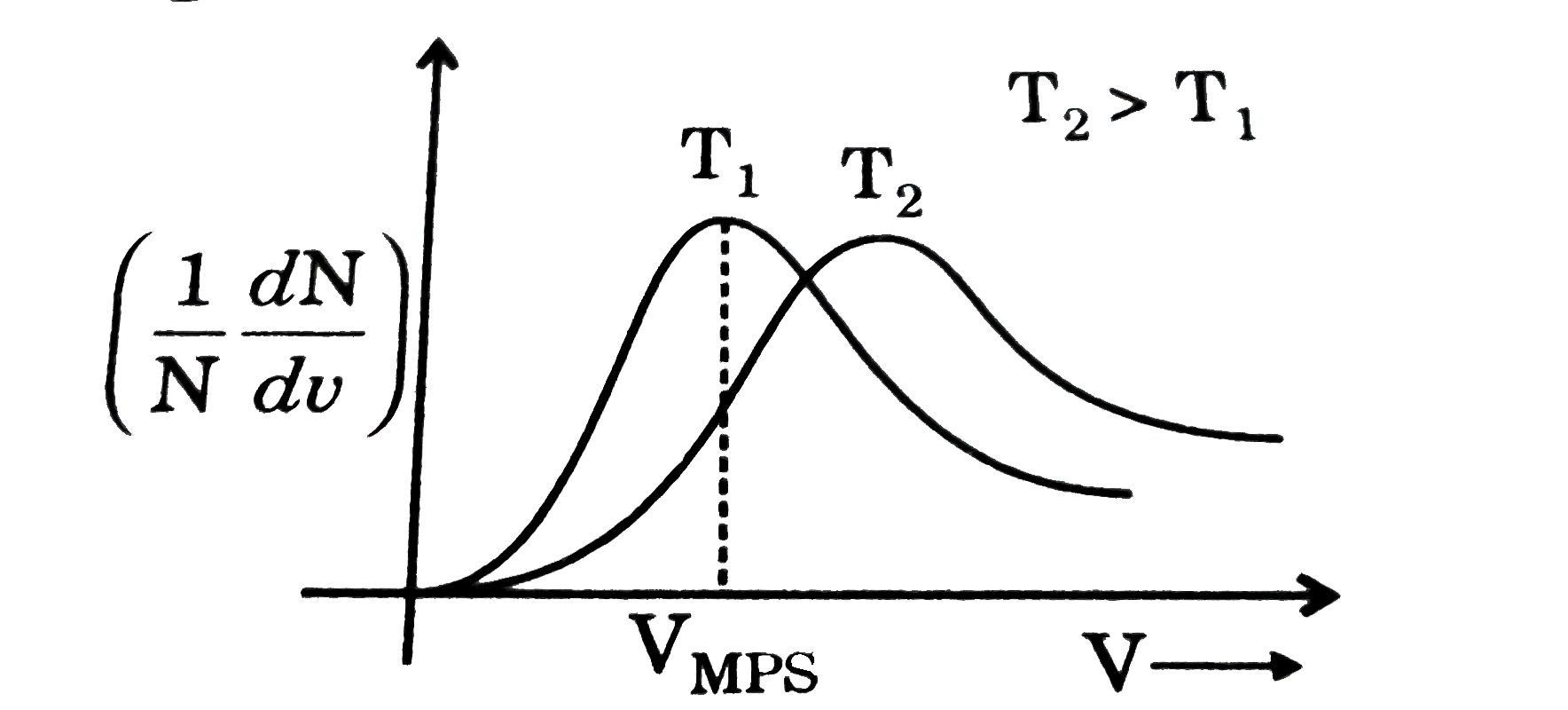
If a gas sample contains a total of N molecules. The area under any given maxwellian plot is equal ot :
View SolutionThe speed of a molecule of a gas changes continuously as a result of collisions with other molecules and with the walls of the container. The speeds of individual molecules therefore change with time.
A direct consequence of the distribution of speeds is that the average kinetric energy is constant for a given temperature.
The average K.E. is defined as
¯¯¯¯¯¯KE=1N(12mΣidNiu21)=12m(ΣidNiN.u21)
where dNN is the fraction of molecules having speeds between ui and ui+du and as proposed by maxwell dNN=4π(m2πKT)3/2exp(−mu22KT).u2.du
The plot of (1NdNdu) is plotted for a particular gas at two different temperature against u as shown.
The majority of molecules have speeds which cluster around vMPS in the middle of the range of v. There area under the curve between any two speeds V1andV2 is the fraction of molecules having speeds betweenV1andV2.
The speed distribution also depends on the mass of the molecules. As the area under the curve is the same (equal to unity) for all gas samples, samples which have the same VMPS will have identical Maxwellian plots. On the basis of the above passage answer the questions that follow.
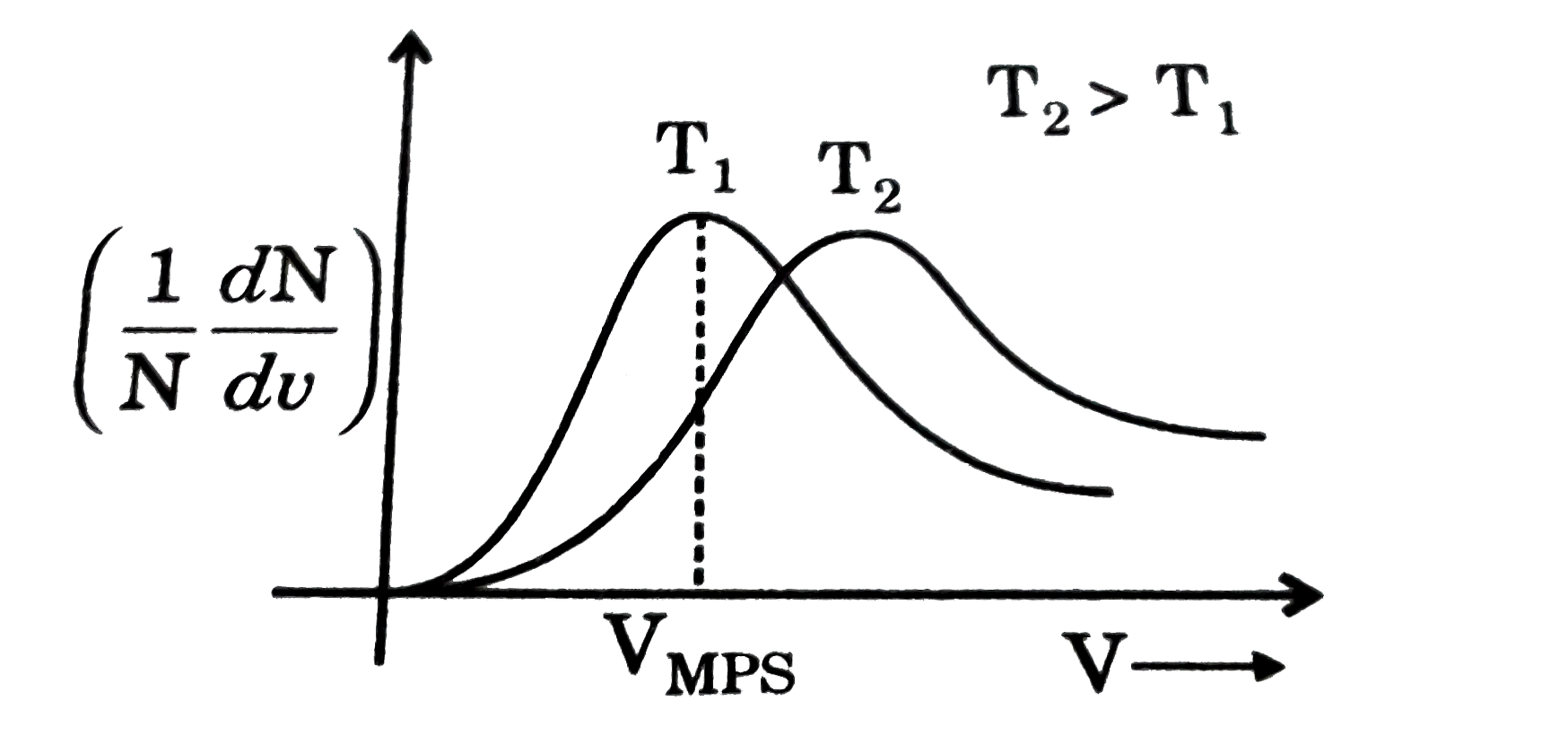
For the above graph, drawn for two different samples of gases at two different temperature T1andT2. Which of the following statements is necessarily true?
View SolutionThe speed of a molecule of a gas changes continuously as a result of collisions with other molecules and with the walls of the container. The speeds of individual molecules therefore change with time.
A direct consequence of the distribution of speeds is that the average kinetric energy is constant for a given temperature.
The average K.E. is defined as
¯¯¯¯¯¯KE=1N(12mΣidNiu21)=12m(ΣidNiN.u21)
where dNN is the fraction of molecules having speeds between ui and ui+du and as proposed by maxwell dNN=4π(m2πKT)3/2exp(−mu22KT).u2.du
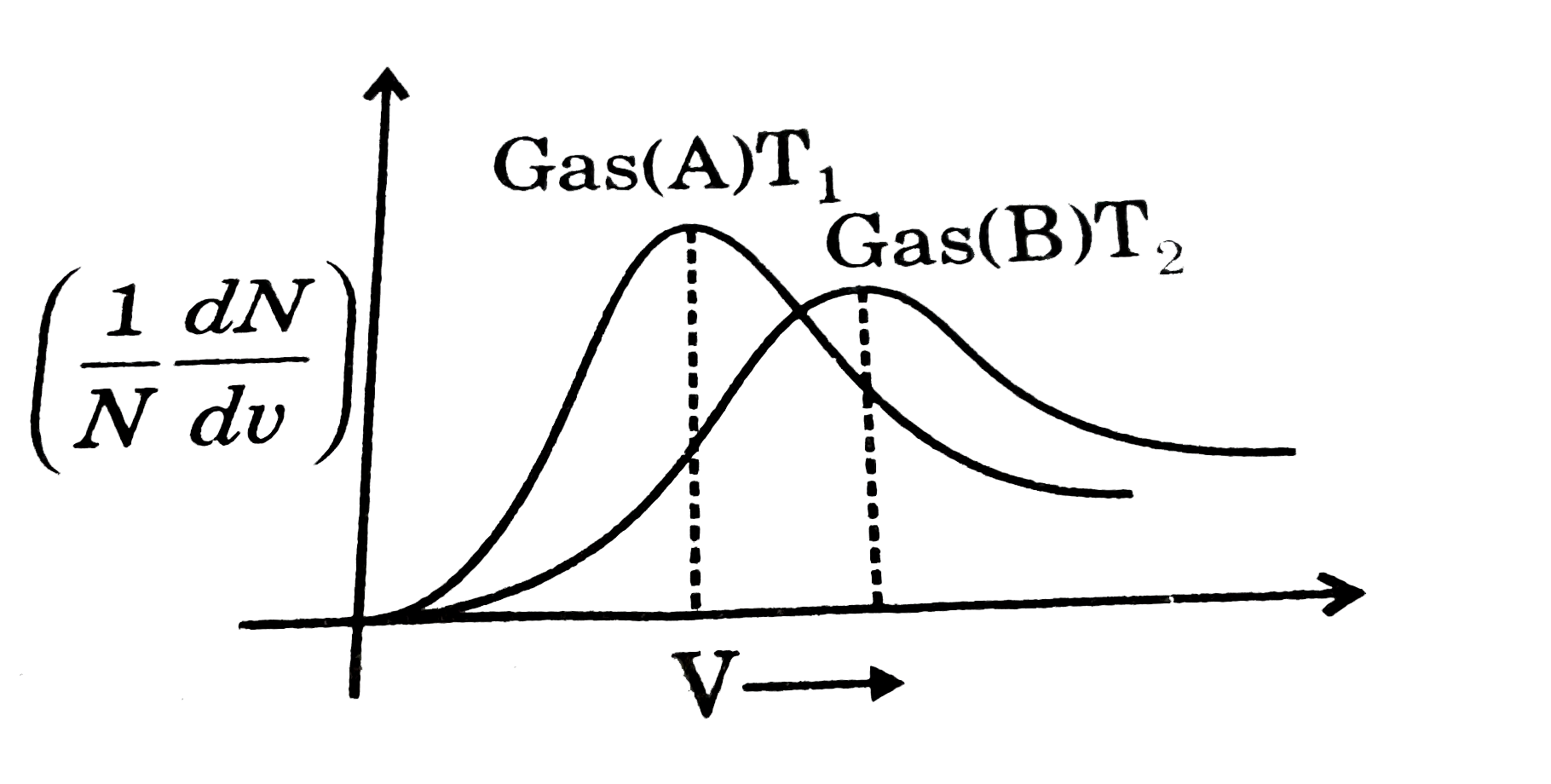
The plot of (1NdNdu) is plotted for a particular gas at two different temperature against u as shown.
The majority of molecules have speeds which cluster around vMPS in the middle of the range of v. There area under the curve between any two speeds V1andV2 is the fraction of molecules having speeds betweenV1andV2.
The speed distribution also depends on the mass of the molecules. As the area under the curve is the same (equal to unity) for all gas samples, samples which have the same VMPS will have identical Maxwellian plots. On the basis of the above passage answer the questions that follow.
If two gases A and B and at temperature TAandTB respectivley have identical Maxwellian plots then which of the following statement are true?
View Solution
