Question

The speed of a molecule of a gas changes continuously as a result of collisions with other molecules and with the walls of the container. The speeds of individual molecules therefore change with time.
A direct consequence of the distribution of speeds is that the average kinetric energy is constant for a given temperature.
The average K.E. is defined as
$\overline{KE}=\frac{1}{N}\left(\frac{1}{2}m\underset{i}{\Sigma }d{N}_i{u}_1^2\right)=\frac{1}{2}m(\underset{i}{\Sigma }\frac{d{N}_i}{N}.u_1^2)$
where $\frac{dN}{N}$ is the fraction of molecules having speeds between $u_i$ and $u_i+du$ and as proposed by maxwell $\frac{dN}{N}=4\pi {\left(\frac{m}{2\pi KT}\right)}^{3/2}\exp (-\frac{{\text{mu}}^2}{2KT}).u^2.du$
The plot of $\left(\frac{1}{N}\frac{dN}{du}\right)$ is plotted for a particular gas at two different temperature against u as shown.
The majority of molecules have speeds which cluster around ${\text{v}}_{\text{MPS}}$ in the middle of the range of v. There area under the curve between any two speeds $V_1\text{and}{V}_2$ is the fraction of molecules having speeds between$V_1\text{and}{V}_2.$
The speed distribution also depends on the mass of the molecules. As the area under the curve is the same (equal to unity) for all gas samples, samples which have the same ${\text{V}}_{\text{MPS}}$ will have identical Maxwellian plots. On the basis of the above passage answer the questions that follow.


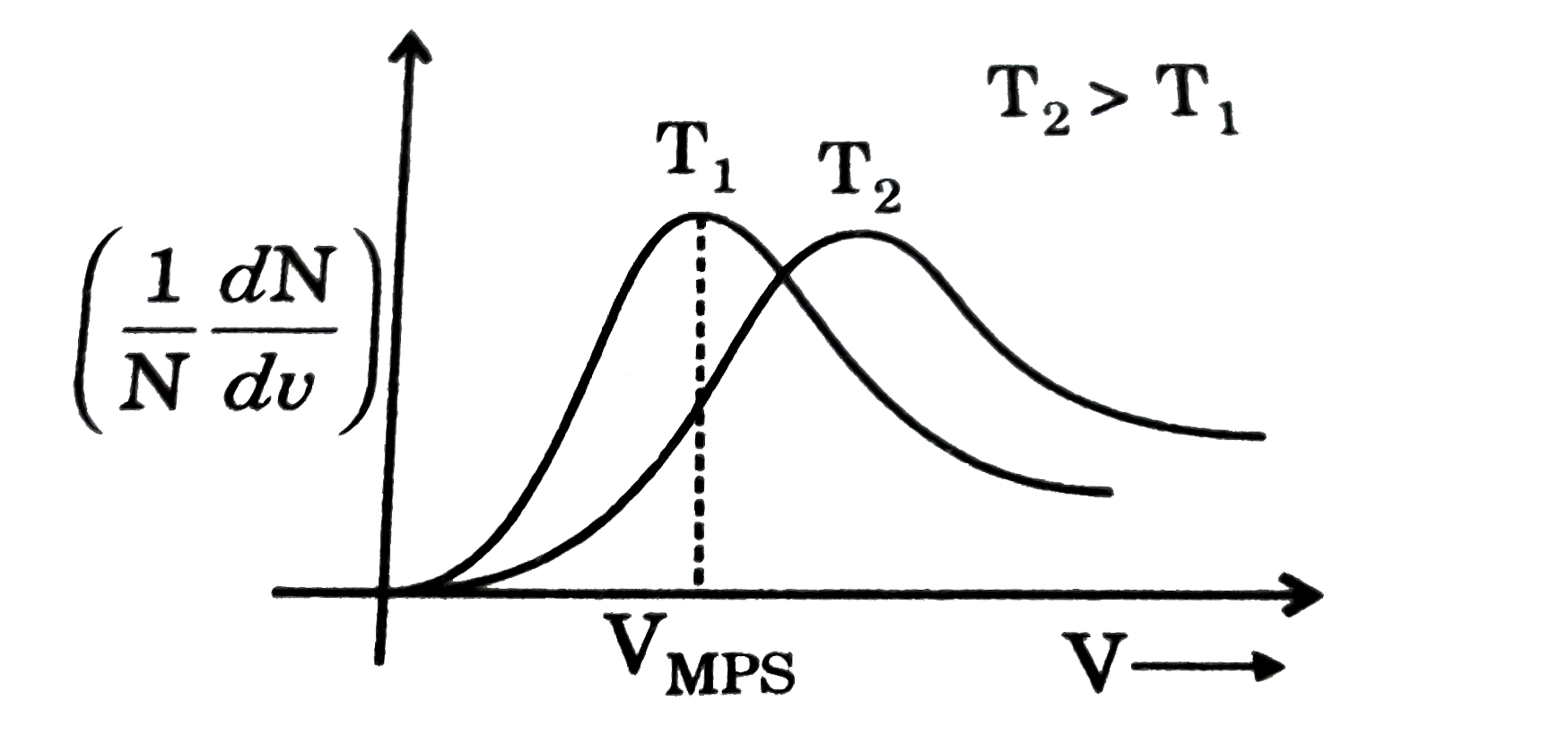
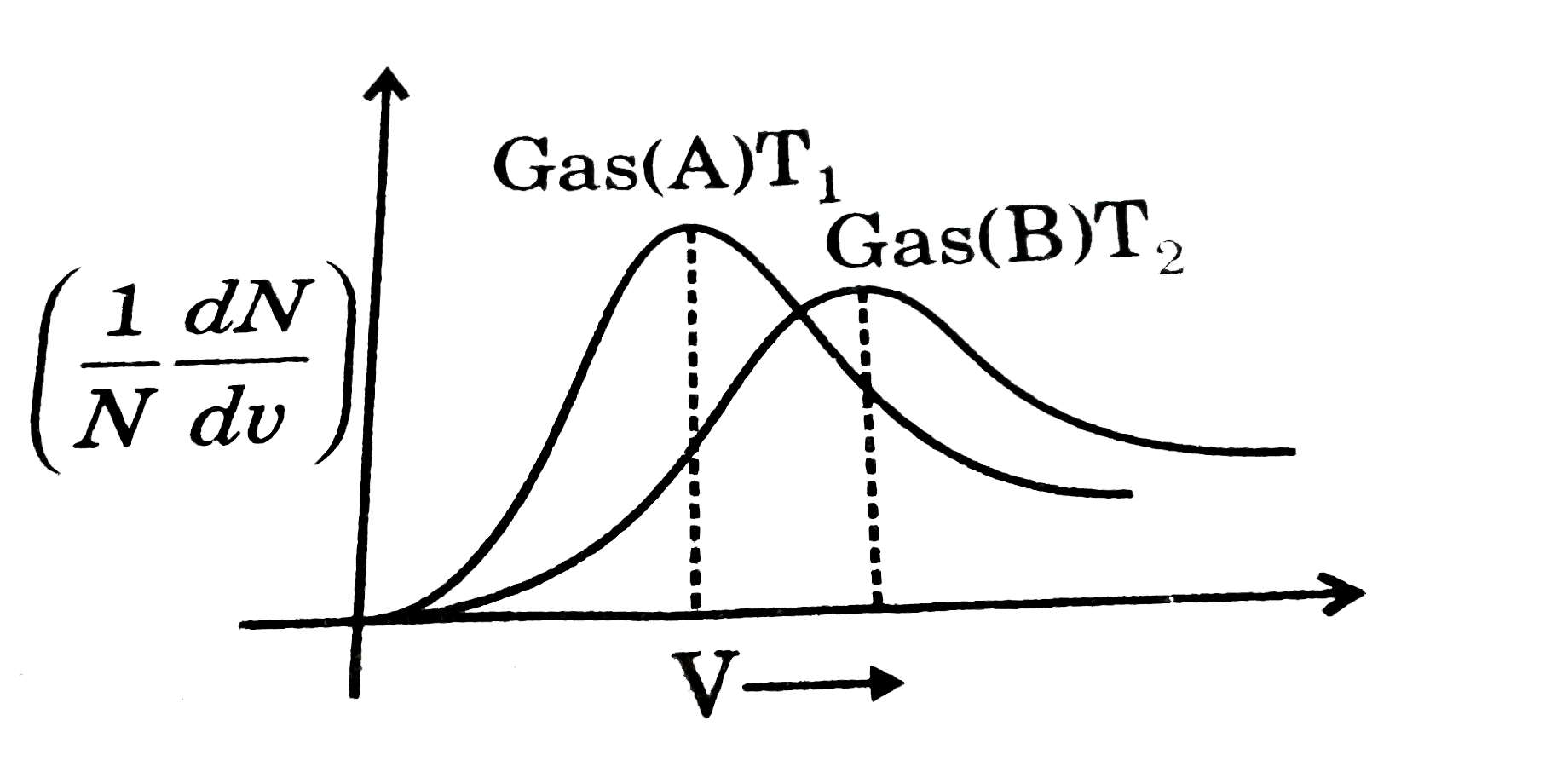
For the above graph, drawn for two different samples of gases at two different temperature $T_1\text{and}{T}_2.$ Which of the following statements is necessarily true?

Options

A. `"If" T_(2) lt T_(1),M_(A) "is necessarily greater than" M_(B)`
B. `"If"T_(1)gt T_(2),M_(B) "is necessarily greater than"M_(A)`
C. `(T_(2))/(M_(B))lt(T_(1))/(M_(A))`
D. Nothing can be predicted

Answer

A