Critical constants for a real gas are given as
$T_{C} = 180 K$ ,
$V_{C} = 0.123 \frac{L}{mole}$
$P_{C} = 45$ atm,
the correct statement for the real gas is:

The actual volume of single gas molecule is $(\frac{0.123 \times 10^{- 3}}{6023 \times 10^{23}})$

$b = 3 \times 0.123 L {mol}^{- 1}$

The Boyle's temperature is less than 180K

Gas cannot be liquefied at 200K

Text Solution

Verified by Experts

The correct Answer is:d

Updated on:21/07/2023

Class 11 CHEMISTRY STATES OF MATTER

Topper's Solved these Questions

Knowledge Check

When pressure is increases at constant temp volume of gas decreases $A B \to g a s e s, B C \to v p o u r + l i q u C D \to l i q u$
critical point: At this point all the physical propeties of liquid phase will be same as the physical properties in vapour such as, density of liquid = density of vapour
$T_{c}$ or critical temp: Temperature abive which a gas can not be liquified
$P_{c}$ or critical pressure: minimum pressure which must be applied at critical temp to convert the gas into liqid.
$V_{c}$ or critical volume: volume occupied by one mole of gas at $T_{c} & P_{c}$
CRITICAL CONSTANT USING VANDERWAAL EQUATIONS:
$\begin{matrix} (P + \frac{a}{V_{m}^{2}}) (V_{m} - g b) = R T & = = \Rightarrow & (P V_{m}^{2} + a) (V_{m} - b) = R T V_{m}^{2} P V_{m}^{3} + a V_{m} - P b V_{m}^{2} - a b - R T V_{m}^{2} = 0 & = = \Rightarrow & V_{m}^{3} + V_{m}^{2} (b + \frac{R T}{P}) + \frac{a}{P} \frac{V}{m} - \frac{a b}{P} = 0 \end{matrix}$
since equation is cubic in $V_{m}$ hence there will be three roots of equation of any temperature and pressure. At critical point all three roots will coincide and will given single value of $V_{m} = V_{c}$ at critical point. Vander Waal equation will be
$V_{m}^{3} - V_{m}^{2} (b + \frac{R T_{C}}{P_{C}}) + \frac{a}{P_{C}} V_{m} - \frac{a b}{P_{C}} = 0 ... (i)$
But at critical point all three roots of the equation should be equal, hence equation should be:
$V_{m} = V_{c}$
${(V_{m} - V_{c})}_{m}^{3} = 0$
$V_{m}^{3} - 3 V_{m}^{2} V_{c} + 3 V_{m} V_{c}^{2} - V_{c}^{3} = 0 . . (2)$
comparing with equation (1)
$b + \frac{R T_{c}}{P_{c}} = 3 V_{c}$ ...(i) $\frac{a}{P_{c}} = 3 V_{c}^{2}$ ...(ii) $\frac{a b}{P_{c}} = V_{c}^{3}$ ..(iii)
From (ii) and (iii), $V_{c} = 3 b$
From (ii) $P_{c} = \frac{a}{3 V_{c}^{2}}$ substituting $P_{c} = \frac{a}{3 {(3 b)}^{2}} = \frac{a}{27 b^{2}}$
From (i) $\frac{R T_{c}}{P_{c}} = 3 V_{c} - b = 9 b - b = 8 b \Rightarrow T_{c} = \frac{8 a}{27 R b}$
At critical point, the slope of $P V$ curve (slope of isotherm) will be zero at all other point slope will be negative zero is the maximum value of slope.
${(\frac{\partial P}{\partial V_{m}})}_{T C} = 0 . . (i) \frac{\partial}{\partial V_{m}} {(\frac{\partial P}{\partial V_{m}})}_{T C} = 0 ... (i i)$
{Mathematically such points an known as point of inflection (where first two derivatives becimes zero)}
using the two $T_{c} P_{c}$ and $V_{c}$ can be calculated by

If the critical constants for a hypotentical gas are $V_{c} = 150 c m^{3} m o l^{- 1} . P_{c} = 50 a t m$ and $T_{c} = 300 K$ . then the radius of the molecule is: [Take $R = \frac{1}{12} L t r a t m m o l^{- 1} K^{- 1}]$
A ${(\frac{75}{2 π N_{A}})}^{1 / 3}$
B ${(\frac{75}{8 π N_{A}})}^{1 / 3}$
C ${(\frac{3}{π N_{A}})}^{1 / 3}$
D ${(\frac{3}{256 π N_{A}})}^{1 / 3}$
The critical constants $P_{C} & T_{C}$ for methane are 45 atm and 180 K. The correct statement is -
A $V_{C} = 2.4 L$
B $b = 0.04 L / m o l$
C $V_{C} = 0.8 L$
D $b = 0.8 L / m o l$
If critical temperature for the real gas is 500 K then the value of :

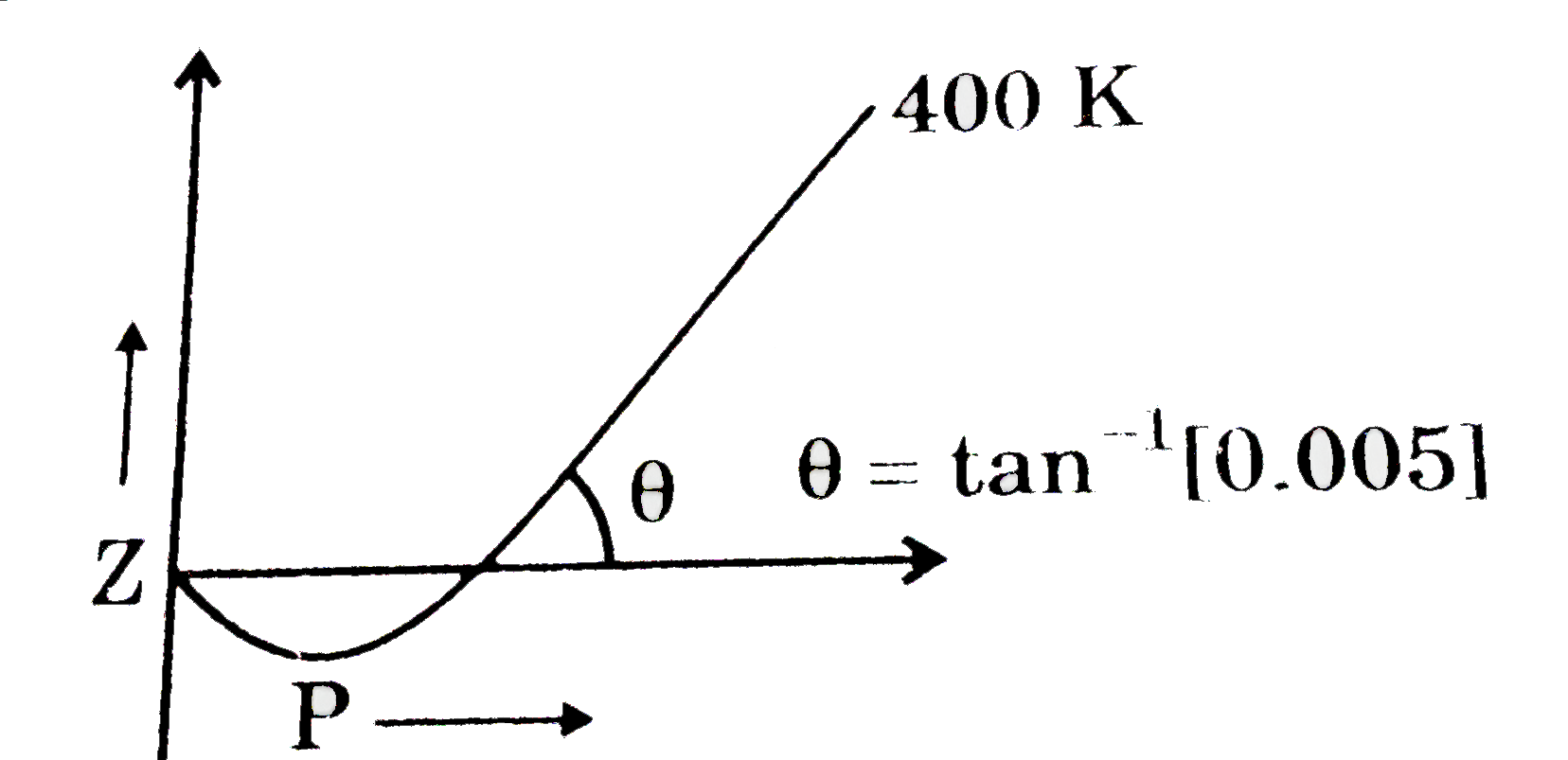ABoyle's temperature is 1687.5K
Bvan der Waals' constant a for the gas is 21.6 atm- $L^{2} / {mol}^{2}$
CGas will show ideal behaviour at high temperature and low pressure
DAt Boyle's temperature behaviour of gas is always ideal

Critical constants for a real gas are given as
$T_{C} = 180 K$ ,
$V_{C} = 0.123 \frac{L}{mole}$
$P_{C} = 45$ atm,
the correct statement for the real gas is:

The correct Answer is:d

Topper's Solved these Questions

Similar Questions

Knowledge Check

The critical constants $P_{C} & T_{C}$ for methane are 45 atm and 180 K. The correct statement is -

If critical temperature for the real gas is 500 K then the value of :

GRB PUBLICATION-GASEOUS STATE-Exercise

Critical constants for a real gas are given as T C = 180 K , V C = 0.123 L mole P C = 45 atm, the correct statement for the real gas is:

The correct Answer is:d

Topper's Solved these Questions

Similar Questions

Knowledge Check

The critical constants PC&TC for methane are 45 atm and 180 K. The correct statement is -

If critical temperature for the real gas is 500 K then the value of :

GRB PUBLICATION-GASEOUS STATE-Exercise

Critical constants for a real gas are given as
$T_{C} = 180 K$ ,
$V_{C} = 0.123 \frac{L}{mole}$
$P_{C} = 45$ atm,
the correct statement for the real gas is:

The critical constants $P_{C} & T_{C}$ for methane are 45 atm and 180 K. The correct statement is -