Two rectangular blocks A and B of different metals have same length and same area of cross-section. They are kept in such a way that their cross-sectional area touch each other. The temperature at one end of A is 100∘C and B at the other end is 0∘C. If the ratio of their thermal conductivity is 1:3, then under steady state, the temperature of the junction in contact will be
25∘C
50∘C
75∘C
100∘C
The correct Answer is:A
Step by step video, text & image solution for Two rectangular blocks A and B of different metals have same length and same area of cross-section. They are kept in such a way that their cross-sectional area touch each other. The temperature at one end of A is 100^(@)C and B at the other end is 0^(@)C. If the ratio of their thermal conductivity is 1 : 3, then under steady state, the temperature of the junction in contact will be by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Topper's Solved these Questions
- BOOK - ERRORLESS CHAPTER - TRANSMISSION OF HEATEXERCISE - Convection13videos
TRANSMISSION OF HEAT
- BOOK - ERRORLESS CHAPTER - TRANSMISSION OF HEATEXERCISE - Radiation (General, Kirchoff s law, Black body)38videos
TRANSMISSION OF HEAT
- BOOK - ERRORLESS CHAPTER - THERMOMETRY, THERMAL EXPANSION AND CALORIMETRY EXERCISE - Self Evaluation Test15videos
THERMOMETRY, THERMAL EXPANSION AND CALORIMETRY
- BOOK - ERRORLESS CHAPTER - UNITS, DIMENSION & MEASUREMENTSEXERCISE - All Questions333videos
UNITS, DIMENSION & MEASUREMENTS
Similar Questions
Three bars of equal lenghts and equal area of cross-section are connected in series. Their thermal conductivities are in the ratio of 2:4:3. If the open ends of the first and the last bars are at temperature 200∘C and 180∘C respectivity in the steady state, calculate the temperature of both the junctions.
View SolutionThree bars of equal lengths x and equal area of cross-section A are connected in series. Their thermal conductivities are in the ratio 2:4:3. If the open ends of the first and the last bars are at temperatures 200∘C and 18∘C, respectively in the steady state, calculate the temperatures of both the junctions.
View Solution
Knowledge Check
- Question 1 - Select One
A metallic prong consists of 4 rods made of the same material, cross-section and same lengths as shown. The three forked ends are kept at 100∘C and the handle end is at 0∘C. The temperature of the junction is
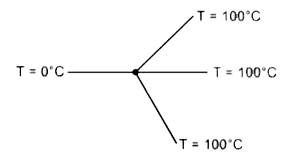 A25∘CB50∘CC60∘CD75∘C
A25∘CB50∘CC60∘CD75∘C - Question 2 - Select One
The length of the two rods made up of the same metal and having the same area of cross-section are 0.6 m and 0.8 m respectively. The temperature between the ends of first rod is 90∘ C and 60∘ C and that for the other rod is 150 and 110∘ C. For which rod the rate of conduction will be greater
AFirstBSecondCSame for bothDNone of the above - Question 3 - Select One
Two rods having thermal conductivity in the ratio of 5 : 3 having equal lengths and equal cross-sectional area are joined by face to face. If the temperature of the free end of the first rod is 100∘C and free end of the second rod is 20∘C . Then temperature of the junction is
A70∘CB50∘CC50∘CD90∘C
Two rods of similar area of cross section and length are joined as shown in the figure. The ratio of their thermal conductivity is 2:3. The free ends are maintained at 100∘C and 0∘C respectivley. THE temperature at junction in steady state is
 View Solution
View SolutionTwo rods are connected as shown. The rods are of same length and same cross sectional area. In steady state, the temperature (θ) of the interface will be -
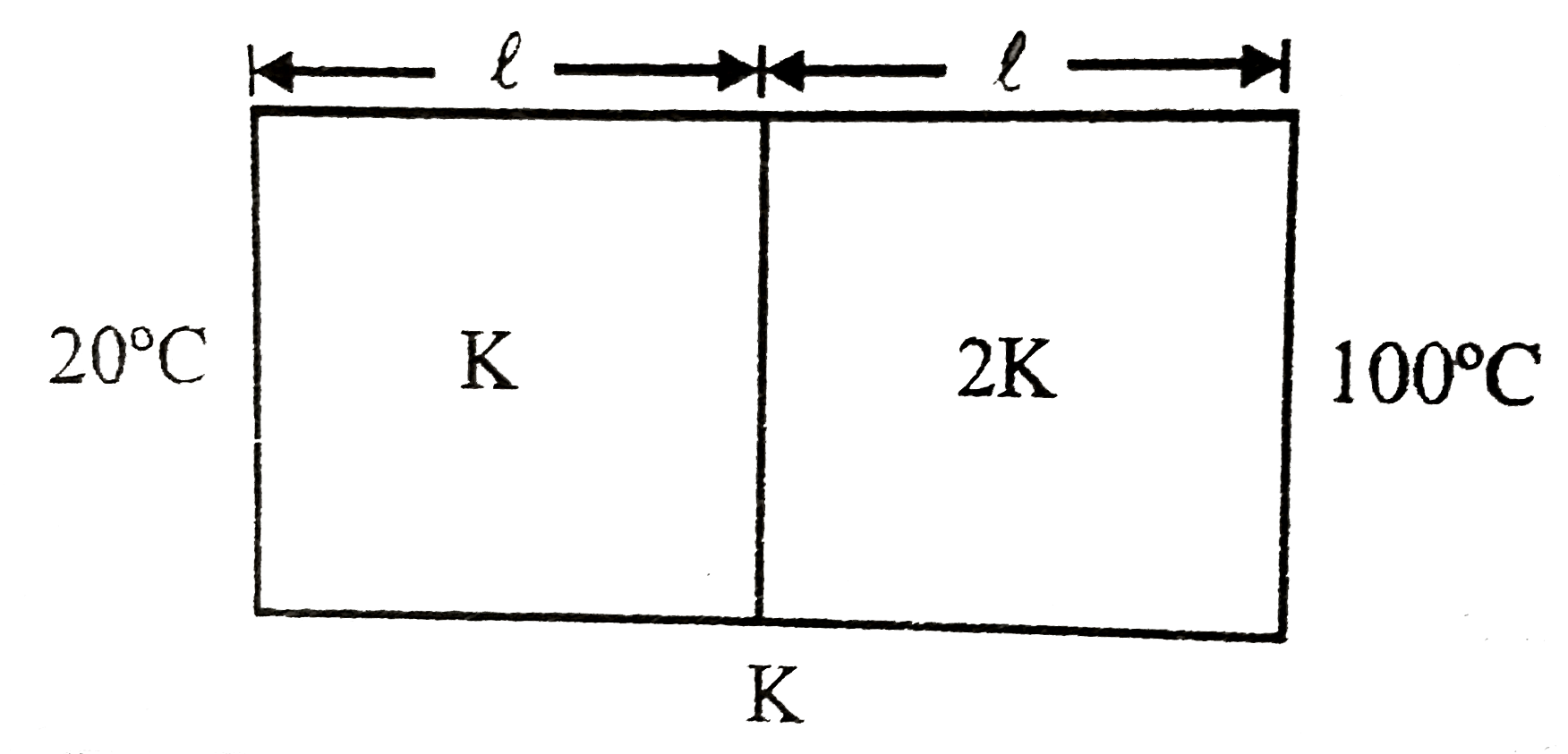 View Solution
View SolutionTwo wires A and B have the same length and area of cross-section. But Young's modulus of A is two times the Young's modulus of B. Then the ratio of force constant of A to that of B is
View SolutionThree rods A, B and C of the same length and same cross-sectional area are joined as shown. Their thermal conductivities are in the ratio 1:2:3/2. If the open ends of A and C are at 200∘C and 18∘C, respectively, then the temperature at the junction of A at steady state is
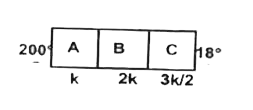 View Solution
View SolutionThree rods A,B and C of the same length and cross- sectional area are joined in series as shown. The temperature at the junction of A and B, in equilibriu, is
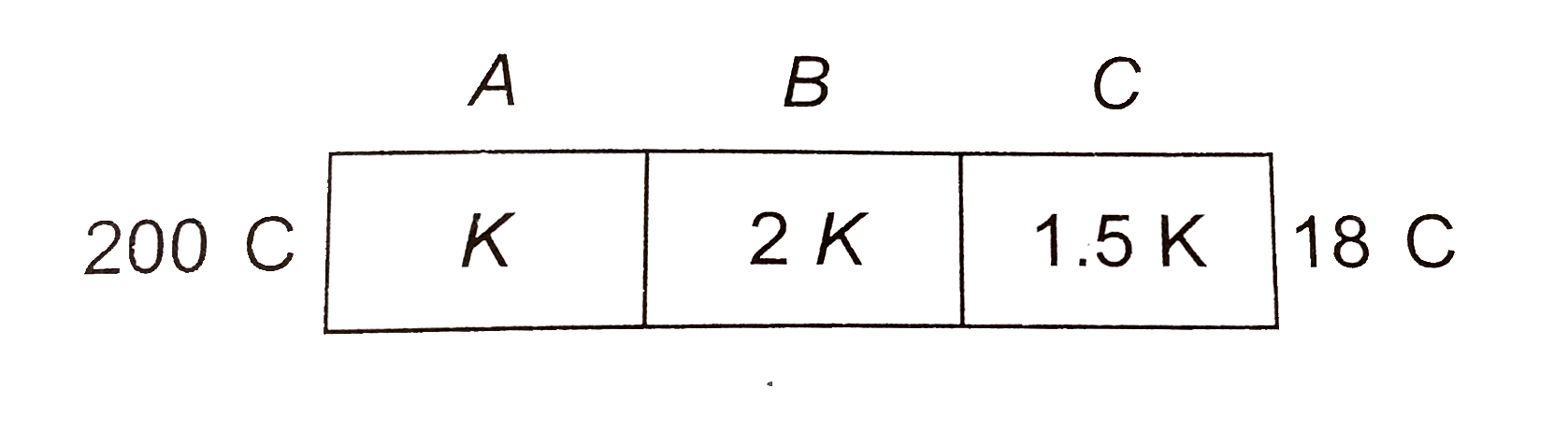 View Solution
View Solution

