A rod of 40 cm in length and temperature difference of 80∘C at its two ends. Another rod B of length 60cm and of temperature difference 90∘C, having the same area of cross-section. If the rate of flow of heat is the same, then the ratio of their thermal conductivities will be
3:4
4:3
1:2
2:1
The correct Answer is:A
Step by step video, text & image solution for A rod of 40 cm in length and temperature difference of 80^(@)C at its two ends. Another rod B of length 60cm and of temperature difference 90^(@)C, having the same area of cross-section. If the rate of flow of heat is the same, then the ratio of their thermal conductivities will be by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
- TRANSMISSION OF HEATBook:ERRORLESS Chapter:TRANSMISSION OF HEATExercise:Assertion & Reason
Explore 24 Videos
- THERMOMETRY, THERMAL EXPANSION AND CALORIMETRY Book:ERRORLESS Chapter:THERMOMETRY, THERMAL EXPANSION AND CALORIMETRY Exercise:Self Evaluation Test
Explore 15 Videos
- UNITS, DIMENSION & MEASUREMENTSBook:ERRORLESS Chapter:UNITS, DIMENSION & MEASUREMENTSExercise:All Questions
Explore 333 Videos
Similar Questions
The temperature difference between two ends of a 2 m long bar A is 40∘C and that between a 3 m long bar B of same area is 60∘C . If the rate of conduction of heat in two bars is same, calculate the ratio of coefficients of thermal conductivity of two bars.
View SolutionWhat is the temperature of steel-copper jumction in the steady state of the system shown in fig. Length of the steel rod = 30.0 cm, length of the copper rod = 20.0 cm, temperature of the furnace = 300∘C, temperature of cold end =0∘C . The area of cross-section of the steel rod is twice that of the copper rod. thermal conductivity of steel = 50.2Js−1m−1.∘C−1 and of copper = 358Js−1m−1.∘C−1.
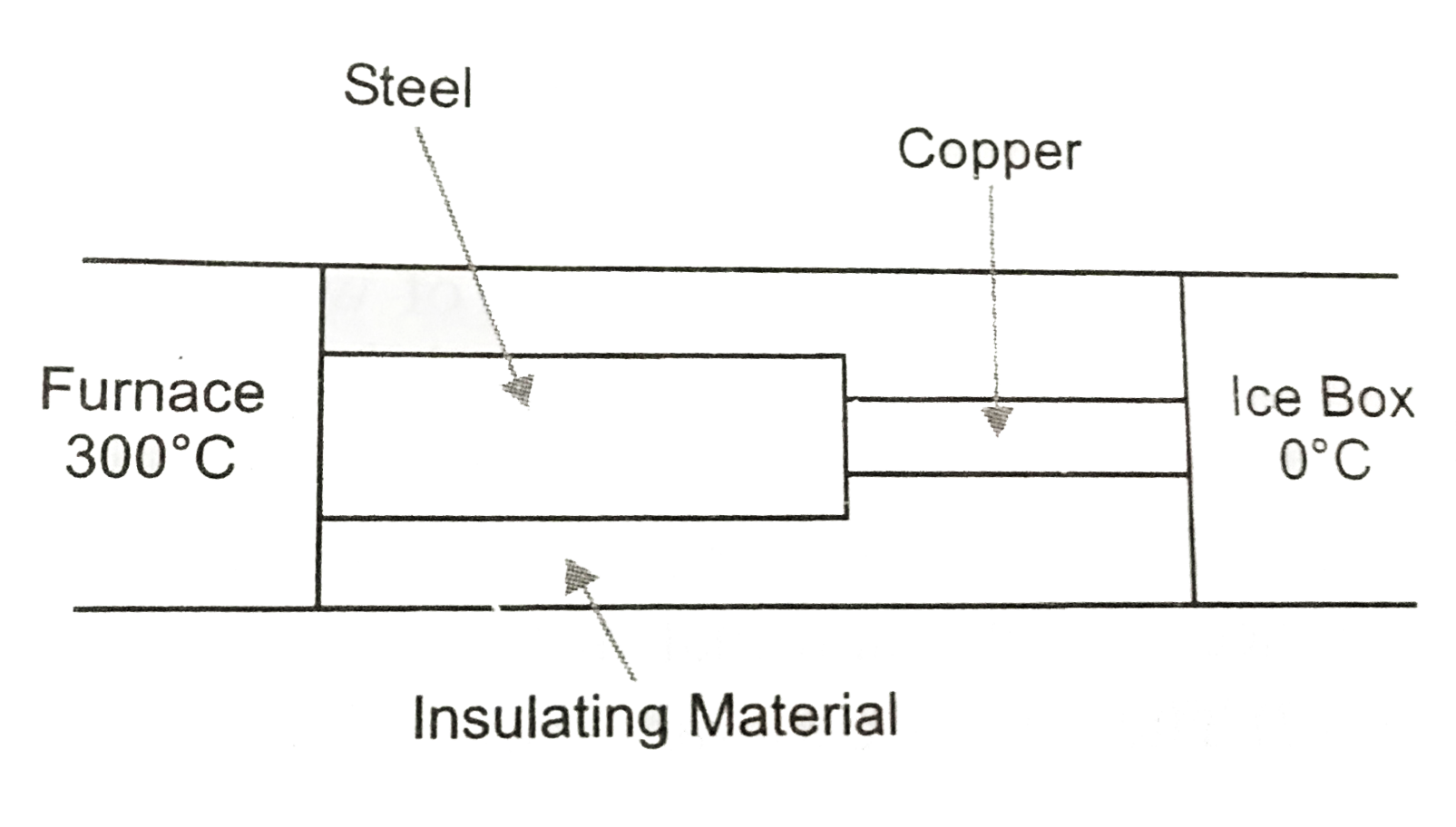
View Solution
Knowledge Check
The ratio of the diameters of two metallic rods of the same material is 2:1 and their lengths are in the ratio 1:4. If the temperature difference between their ends are equal, the rate of flow of heat in them will be in the ratio
A2:1B4:1C8:1D16:1Wires A and B have have identical lengths and have circular cross-sections. The radius of A is twice the radius of B i.e. RA=2RB. For a given temperature difference between the two ends, both wires conduct heat at the same rate. The relation between the thermal conductivities is given by-
AKA=4KBBKA=2KBCKA=KB/2DKA=KB/4The ratio of thermal conductivity of two rods of different material is 5:4. The two rods of same area of cross-section and same thermal resistance will have the lengths in the ratio
A4:5B9:1C1:9D5:4
Temperature difference of 120∘C is maintained between two ends of a uniform rod AB of length 2L. Another bent rod PQ, of same cross-section as AB and length3L2, is connected across AB (See figure). In steady state, temperature difference between P and Q will be close to :

View SolutionIn the following situations, the length and area of cross-section of each rod is same. Find temperature θ at junction of rods.
(a)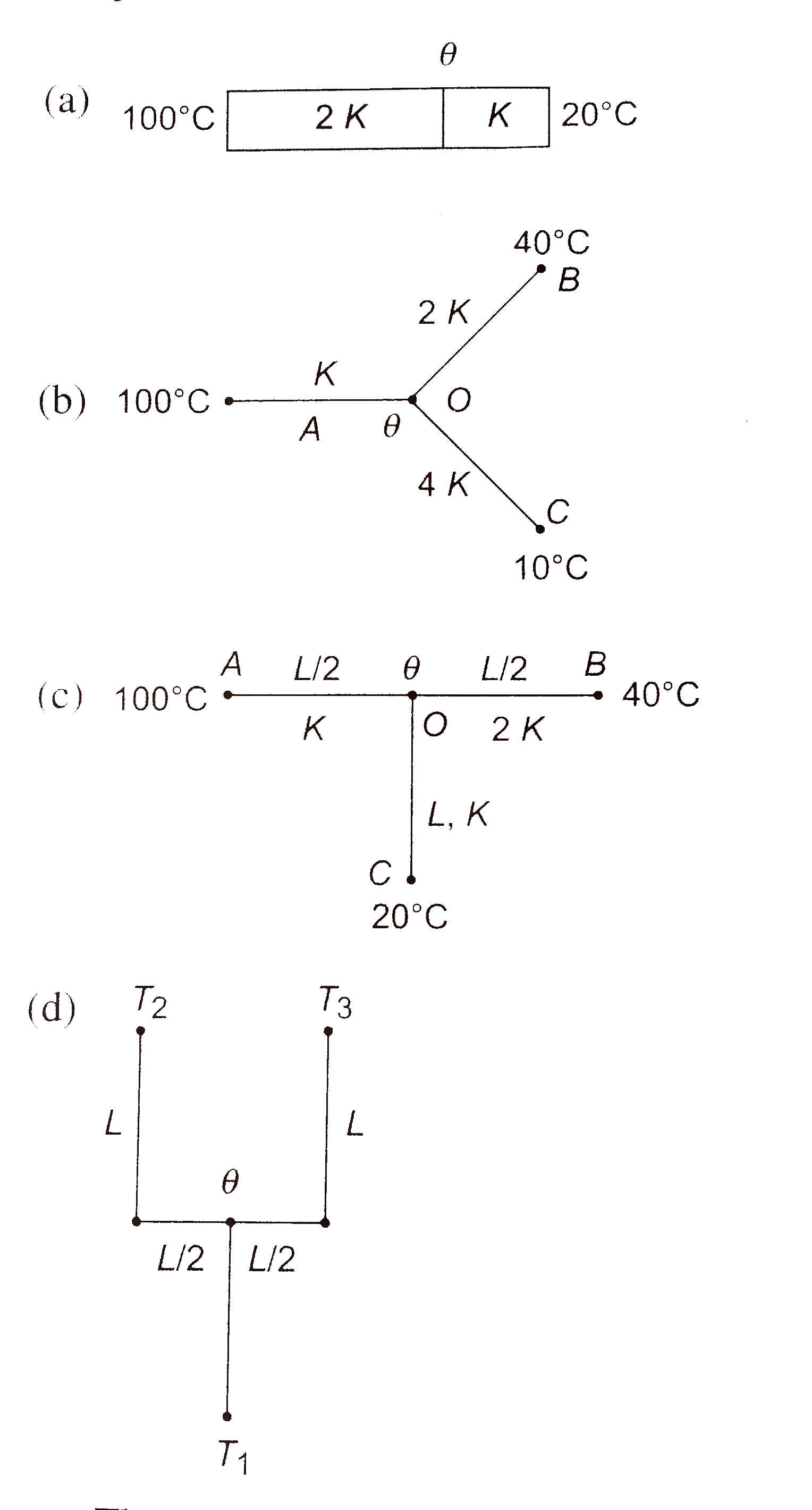
(b)
(c )
(d)
The thermal conductivity of each rod is K.
View SolutionTwo rods of length l and 2l thermal conductivities 2K and K are connected end to end. If cross sectional areas of two rods are eual, then equivalent thermal conductivity of the system is .
View SolutionA metal rod of area of cross section A has length L and coefficient of thermal conductivity K the thermal resistance of the rod is .
View SolutionThree metal rod A, B and C of same length and cross-section are placed end to end and a temperature difference is maintained between the free ends of A and C. If the thermal conductivity of B(KB) is twice that of C(KC) and half that of A(KA), then the effective thermal conductivity of the system will be
View Solution