Identify the option representing correct set of true/false statements:
Statements-1: TiO3 can behve as conductor or insulator depending upon temperature.
Statement-2: CrO2 has electrical properties like metals.
Statements-3: AgBr can shows both frenkel as well as Schottky defects
All the statements are correct
Only statements-3 is correct
Only statements-1 is incorrect
Only statements-2 is correct
Step by step video & image solution for Identify the option representing correct set of true/false statements: Statements-1: TiO_(3) can behve as conductor or insulator depending upon temperature. Statement-2: CrO_(2) has electrical properties like metals. Statements-3: AgBr can shows both frenkel as well as Schottky defects by Chemistry experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
Each question has four choices a,b,c and d out of which only one is correct. Each question contains Statement 1 and Statement 2. Make your answer as: If both the statements are true and Statement 2 is the correct explanation of statement 1. If both the statements are True but Statement 2 is not the correct explanation of Statement 1. If Statement 1 is True and Statement 2 is False. If Statement 1 is False and Statement 2 is True. Statement 1: sinπ18 is a root of 8x3−6x+1=0 Statement 2: For any θ∈R,sin3θ=3sinθ−4sin3θ
View SolutionEach question has four choices, a,b,c and d,out of which only one is correct. Each question contains STATEMENT 1 and STATEMENT 2. if both the statements are true and statement 2 is the correct explanation of statement 1. If both the statements are true but statement 2 is not the correct explanation of statement 1. If statement is True and statement2 is false. If statement1 is false and statement2 is true. Statement 1: If x∈[1,√3], then the range of f(x)=tan−1x is [π4,π3] Statement 2 : If x∈[a,b], then the range of f(x)is[f(a),f(b)].
View Solution
Knowledge Check
Statement-1: The maximum charge that can be given to a conductor of fixed volume depends on its shape.
Statement-2: If the electric field near the condutor is sufficient for dielectric breakdown of air, no more charge can be transferred to it.AStatement-1 is true, statement-2 is true and statement-2 is correct explanation for statement-1.BStatement-1 is true, statement-2 is true and statement-2 is NOT the correct explanation for statement-1.CStatement-1 is true, statement-2 is false.DStatement -1 is false, statement -2 is true.Assertion: Free redicals are always planer.
Reason: They can achieve sp2 as well as sp3-hybridisationAStatement-1 is True, Statement-2 is True, Statement-2 is a correct explanation for statement-1.BStatement-1 is True, Statement-2 is True, Statement-2 is not a correct explanation for statement-1.CStatement-1 is True, Statement-2 is False.DStatement-1 is False, Statement-2 is False
a. Statement- 1 and Statement- 2 are true, and state-ment- 2 is the correct explanation of Statement- 1.
b. Statement- 1 and Statement- 2 are true but Statement- 2 is not the correct explanation of Statement- 1.
c. Statement- 1 is true and Statement- 2 is false.
d. Statement- 1 is false and Statement- 2 is true.
e. Statement- 1 is false and Statement- 2 is false.
Statement- 1:
Compound (I) is formed not (II).
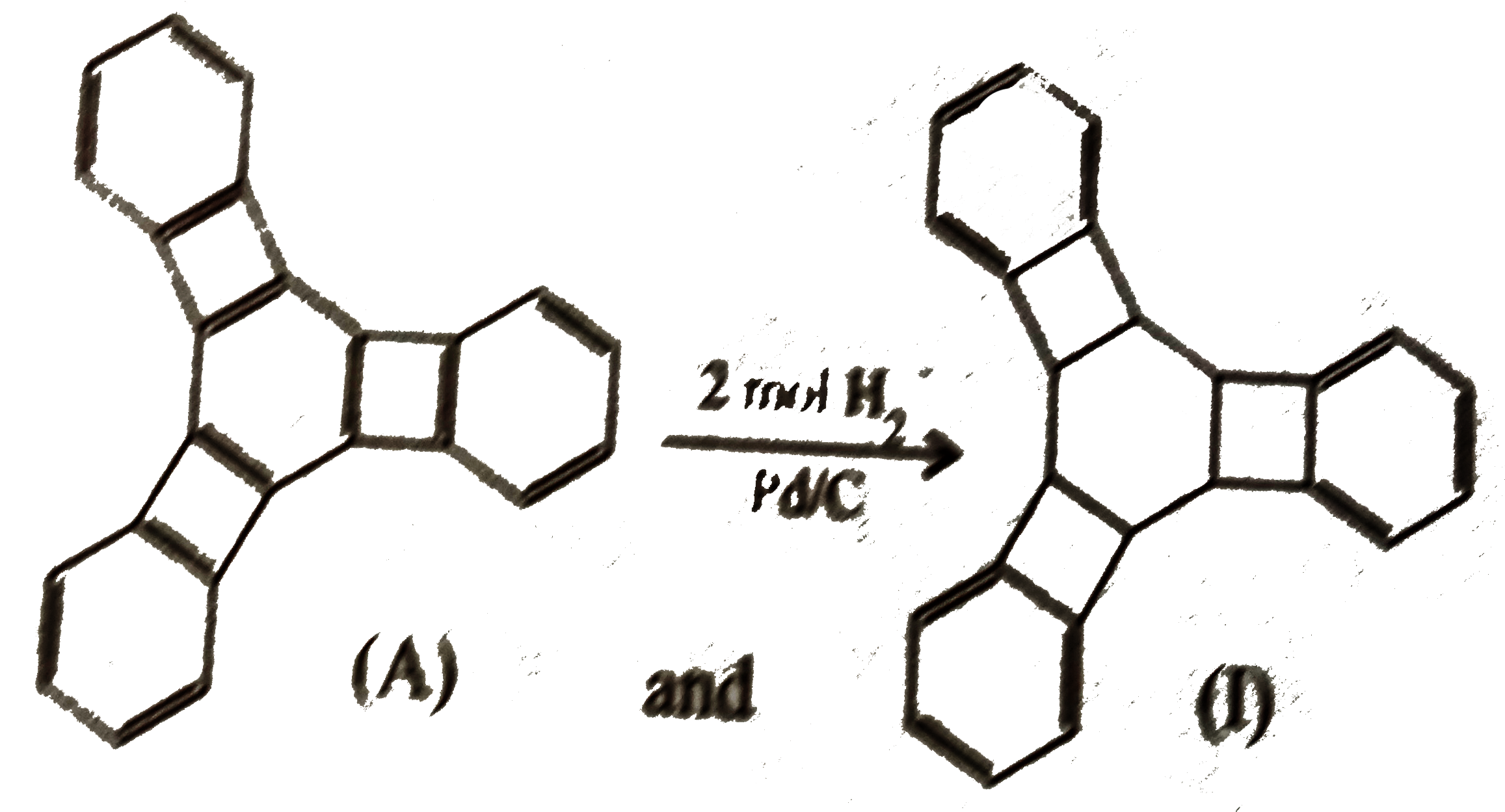 and
and 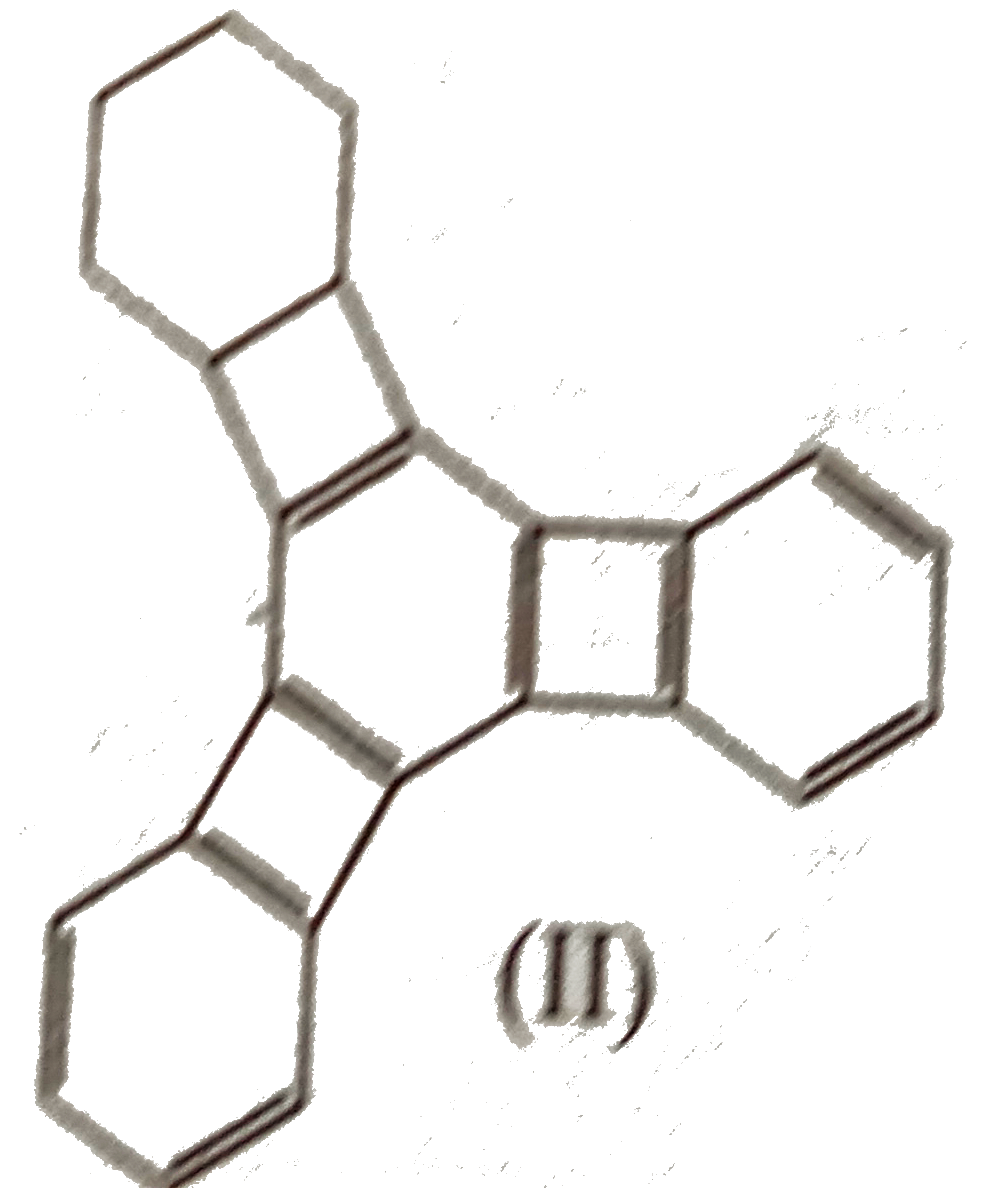
Statement- 2:
Due to the reduction of central ring, 3 four-membered anti-aromatic rings become stable to from (I). In (II), due to the reduction of terminal ring, only one anti-aromatic ring can be stabilised.
View SolutionStatement-1 Let f:[0,∞)−−−→0,∞ be a function defined by y=f(x)=x2, then (d2ydx2)(d2xdy2)=1 Statement-2 d2ydx2=−d2xdy2.dydx3 Statement-1 is True, Statement-2 is True and Statement-2 is correct explanation for Statement-1 Statement-1 is True, Statement-2 is True and Statement-2 is not correct explanation for Statement-1 Statement-1 is True, Statement-2 is false Statement-2 is False, Statement-2 is true Both Statements are false
View SolutionEach question has four choices, a,b,c and d,out of which only one is correct. Each question contains STATEMENT 1 and STATEMENT 2. if both the statements are true and statement 2 is the correct explanation of statement 1. If both the statements are true but statement 2 is not the correct explanation of statement 1. If statement is True and statement2 is false. If statement1 is false and statement2 is true. Consider the function f(x)=sin(kx)+{x}, where (x) represents the fractional part function. Statement 1 : f(x) is periodic for k=mπ, where m is a rational number Statement 2 : The sum of two periodic functions is always periodic.
View SolutionEach question has four choices, a,b,c and d,out of which only one is correct. Each question contains STATEMENT 1 and STATEMENT 2. if both the statements are true and statement 2 is the correct explanation of statement 1. If both the statements are true but statement 2 is not the correct explanation of statement 1. If statement is True and statement2 is false. If statement1 is false and statement2 is true. Statement 1: f:N→R,f(x)=sinx is a one-one function. Statement 2: The period of sinξs2πand2π is an irrational number.
View SolutionEach question has four choices, a,b,c and d,out of which only one is correct. Each question contains STATEMENT 1 and STATEMENT 2. if both the statements are true and statement 2 is the correct explanation of statement 1. If both the statements are true but statement 2 is not the correct explanation of statement 1. If statement is True and statement2 is false. If statement1 is false and statement2 is true. Statement 1: f(x)=(log)ex cannot be expressed as the sum of odd and even function. Statement 2 : f(x)=(log)ex in neither odd nor even function.
View SolutionEach question has four choices, a,b,c and d,out of which only one is correct. Each question contains STATEMENT 1 and STATEMENT 2. if both the statements are true and statement 2 is the correct explanation of statement 1. If both the statements are true but statement 2 is not the correct explanation of statement 1. If statement is True and statement2 is false. If statement1 is false and statement2 is true. Consider the function satisfying the relation if f(2tanx1+tan2x)=((1+cos2x)sec2x+2tanx2 Statement 1: The range of y=f(x)isR. Statement 2: Linear function has rang R if domain is R.
View Solution
