Mr.Santa has to decode a number "ABCDEF" where each alphabet is respersented by a single digit .
Suppose an orbital whose radial wave functoin id respresented as
Ψr=K1.e_r/k2(r2−5k3r+k23)
From the following information given about each alphabet then write down the answer in the from of
"ABCDEF" , for above orbital .
Info A= Value of n where "n" is principle quantum number
Info B= No .of angular nodes
InfoC=Azimuthal quantum number of subshell to orbital belongs
Info D= No. of subshells having energy between (n+5)s to (n+5)p where n id principle quantum
number
Info E=Orbital angular momentum of given orbital.
Info F= Radial distance of the spherical node which is farthest from the nuclues
(Assuming K3 =1)
The correct Answer is:30303
Generalized equation of Ψ(g)
Ψ(r)=4pK1e_r/k2×rl (polynomial)n−l−1
compare the given equantion with the above equation we get
n−l−1=2 .........(i)
l=0 .........(ii)
n=3
and slove accordingly
Topper's Solved these Questions
Similar Questions
Mr. Santa has to decode a number “ABCDEF” where each alphabet is represented by a single digit. Suppose an orbital whose radial wave functional is represented as :
ψ(r)=k1e−r/k2(r2−5k3r+6k23)
From the following information given about each alphabet then write down the answers in the form of “ABCDEF”, for above orbital.
Info A = Value of n where “n” is principal quantum number.
Info B = No. of angular nodes
Info C = Azimuthal quantum number of subshell to orbital belongs
Info D = No. of subshells having energy between (n+5) s to (n+5) p where n is principal quantum number.
Info E = Orbital angular momentum of given orbital.
Info F = Radial distance of the spherical node which is farthest from the nucleus.
(Assuming k3=1))
View SolutionΨr=k1e−r/k2(r2−5k3r+6K23)
For the above orbital match the column-I with column-II (assuming ,k3=1)

View Solution
Knowledge Check
Ψ(r)=ke−r/k1.r2(r2−k2r+k3) . If the orbital has no nodal plane , then , orbital can be :
A5dxyB5dC4dz2D4pxFor an orbital , having no planar angular nodes following the equation :
Ψ(r)=Ke−r/K'.r2(K''−r)
Identify the orbital :A4dz2B2sC3dz2D4dxyFor an orbital the graph between ψ(r) and r (distance from nucles) is :
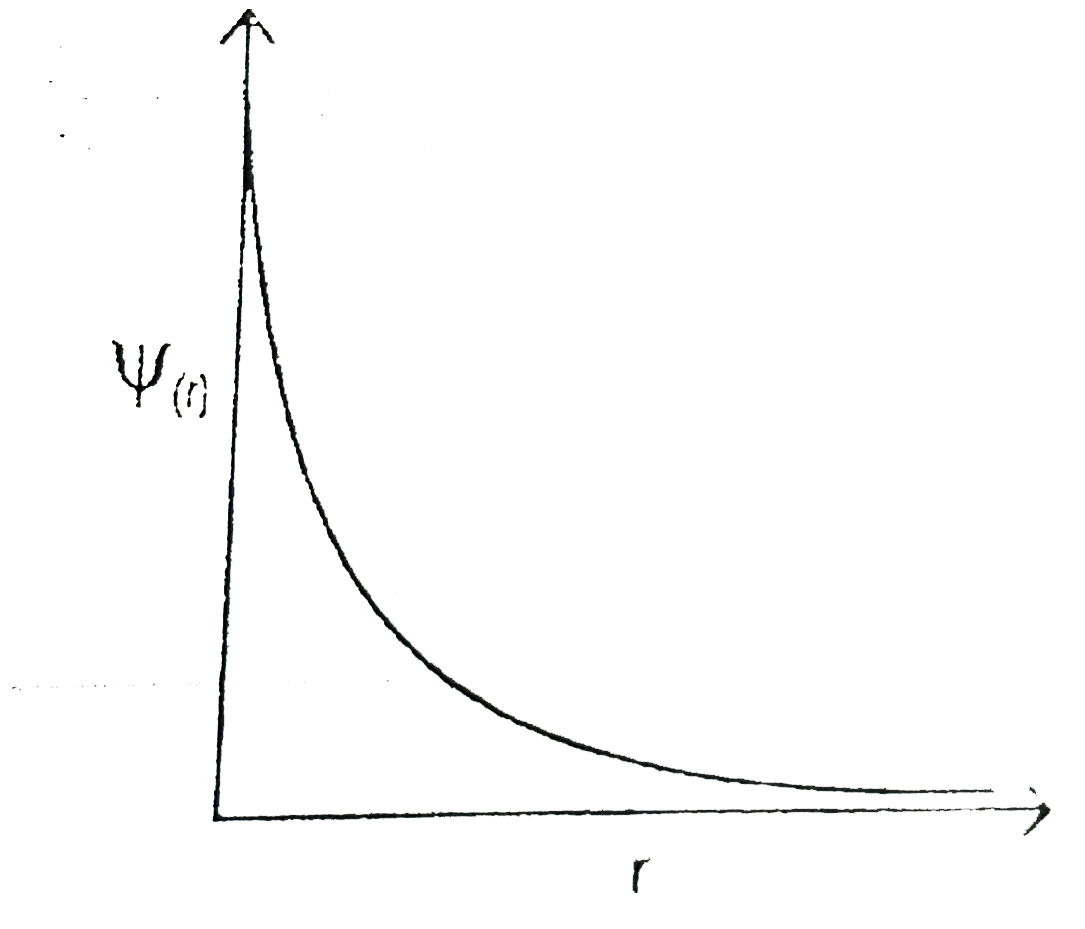
Find the value of n+l of the orbital.A1B2C3DNone of these
k∑r=1(−3)r−1.3nC2r−1=0, where k=3n2 and n is an even integer
View SolutionThe variation of radial probability density R2 (r) as a function of distance r of the electron from the nucleus for 3p orbital:
View SolutionProve thatk∑r=1(−3)r−1C(3n,2r−1)=0, where k=3n2 and n is an even positive integer.
View SolutionIf (n−1)Cr=(k2−3)nCr+1,then k belong to
View SolutionSuppose an electron is attracted toward the origin by a forcekr where k is a constant and r is the distance of the electron from the origin .By applying Bohr model to this system the radius of the nth orbital of the electron is found to be rn and the kinetic energy of the electron to be Tn , Then which of the following is true ?
View Solution
