Mr. Santa has to decode a number “ABCDEF” where each alphabet is represented by a single digit. Suppose an orbital whose radial wave functional is represented as :
$ψ_{(r)} = k_{1} e_{2}^{- r / k_{2}} (r^{2} - 5 k_{3} r + 6 k_{3}^{2})$
From the following information given about each alphabet then write down the answers in the form of “ABCDEF”, for above orbital.
Info A = Value of n where “n” is principal quantum number.
Info B = No. of angular nodes
Info C = Azimuthal quantum number of subshell to orbital belongs
Info D = No. of subshells having energy between $(n + 5)$ s to $(n + 5)$ p where n is principal quantum number.
Info E = Orbital angular momentum of given orbital.
Info F = Radial distance of the spherical node which is farthest from the nucleus.
(Assuming $k_{3} = 1))$

Text Solution

Verified by Experts

The correct Answer is:300303

Updated on:21/07/2023

$Ψ_{(r)} = k e_{1}^{- r / k_{1}} . r^{2} (r^{2} - k_{2} r + k_{3})$ . If the orbital has no nodal plane , then , orbital can be :
A $5 d_{x y}$
B $5 d$
C $4 d_{z^{2}}^{2}$
D $4 p_{x}$
For an orbital , having no planar angular nodes following the equation :
$Ψ_{(r)} = K e^{- r / K'} . r^{2} (K'' - r)$
Identify the orbital :
A $4 d_{z^{2}}^{2}$
B2s
C $3 d_{z^{2}}^{2}$
D $4 d_{x y}$
For an orbital the graph between $ψ_{(r)}$ and $r$ (distance from nucles) is :

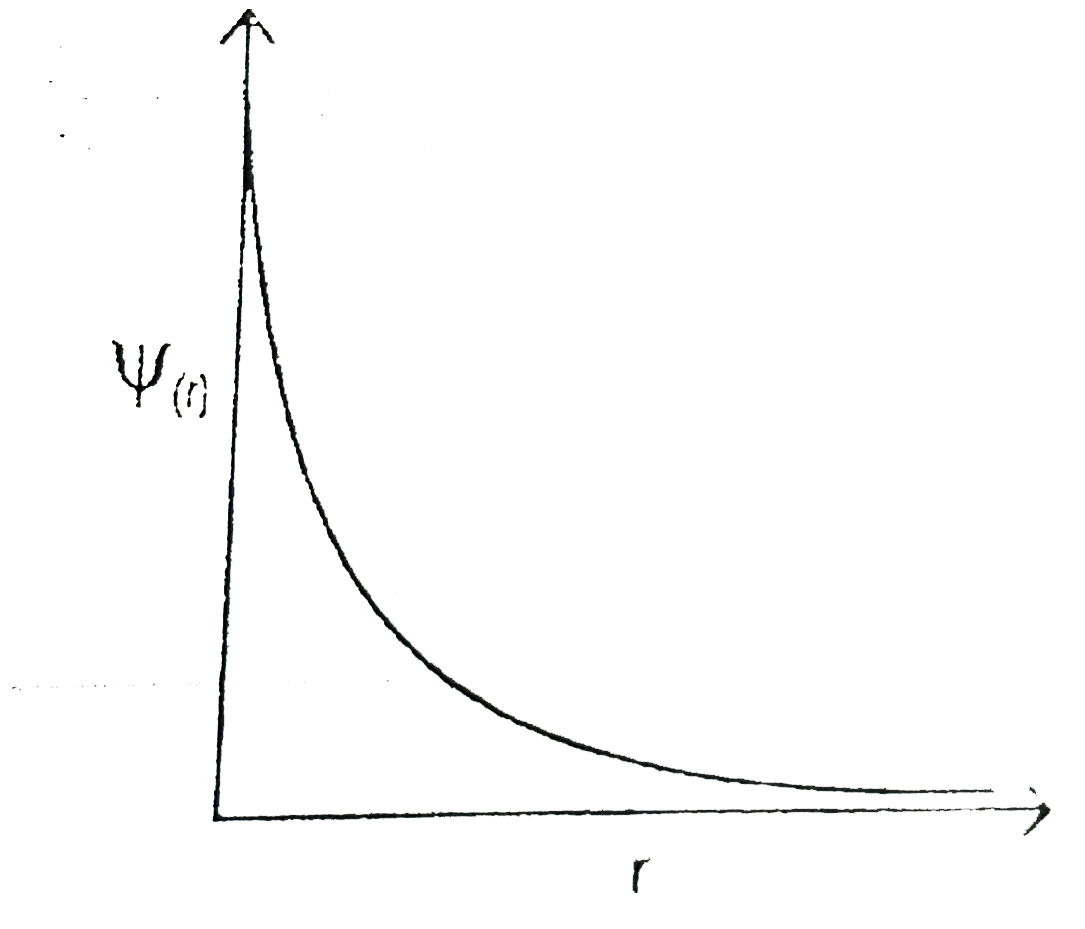
Find the value of $n + l$ of the orbital.
A $1$
B $2$
C $3$
DNone of these