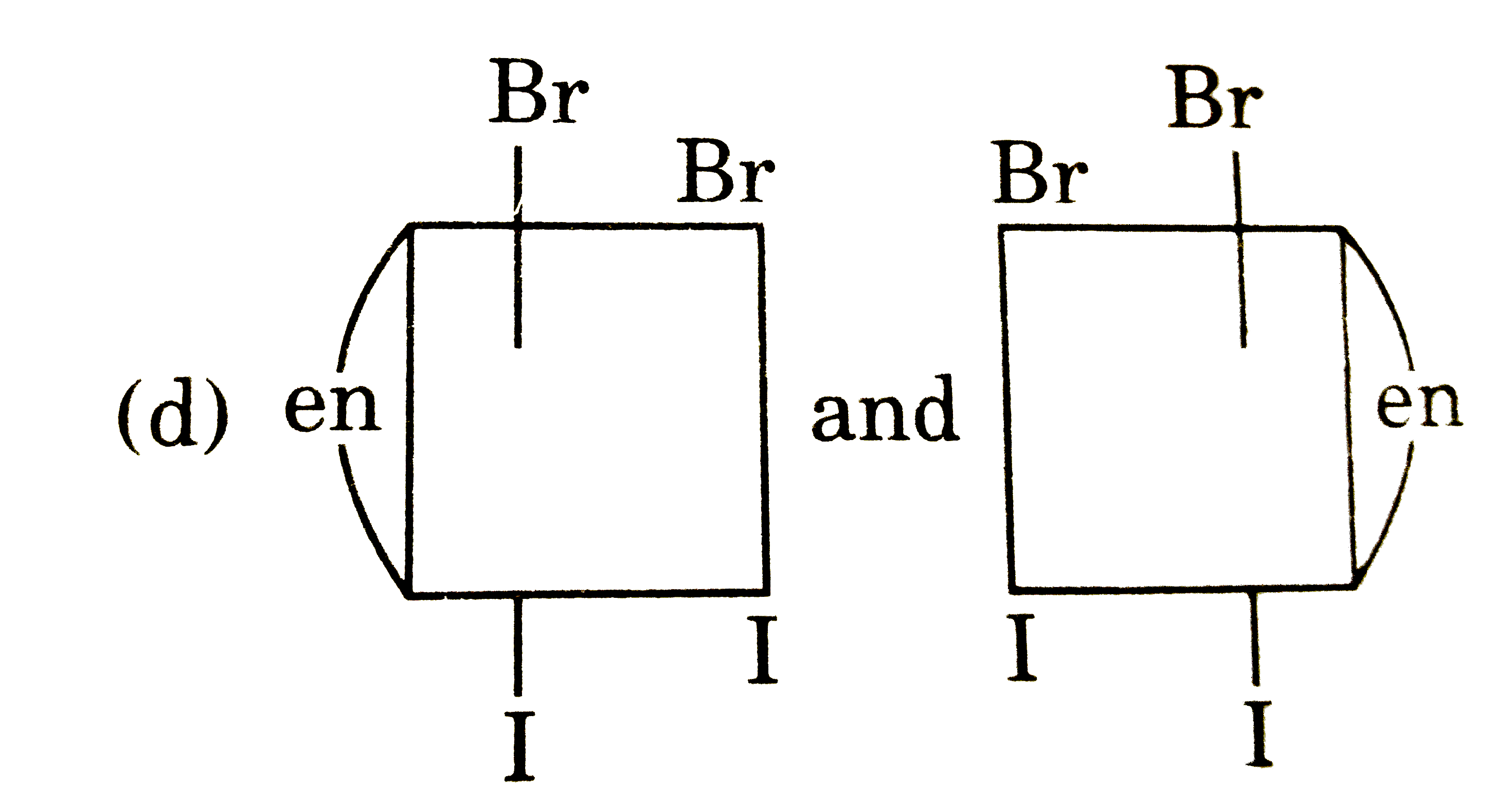
The complex ion . [M(en)Br2I2]−1, has two optical isomers. Their correct configurations are:
A
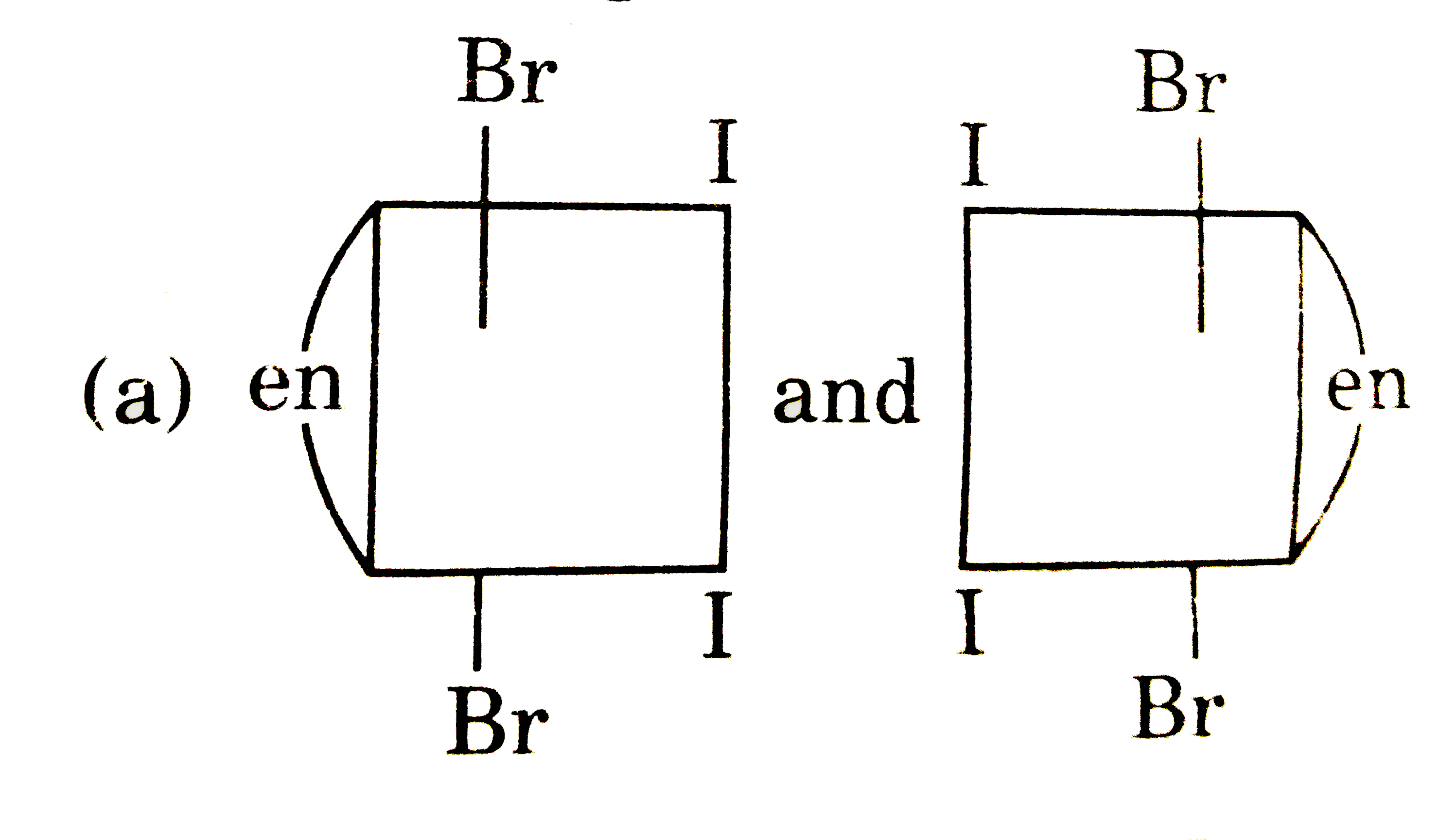
B
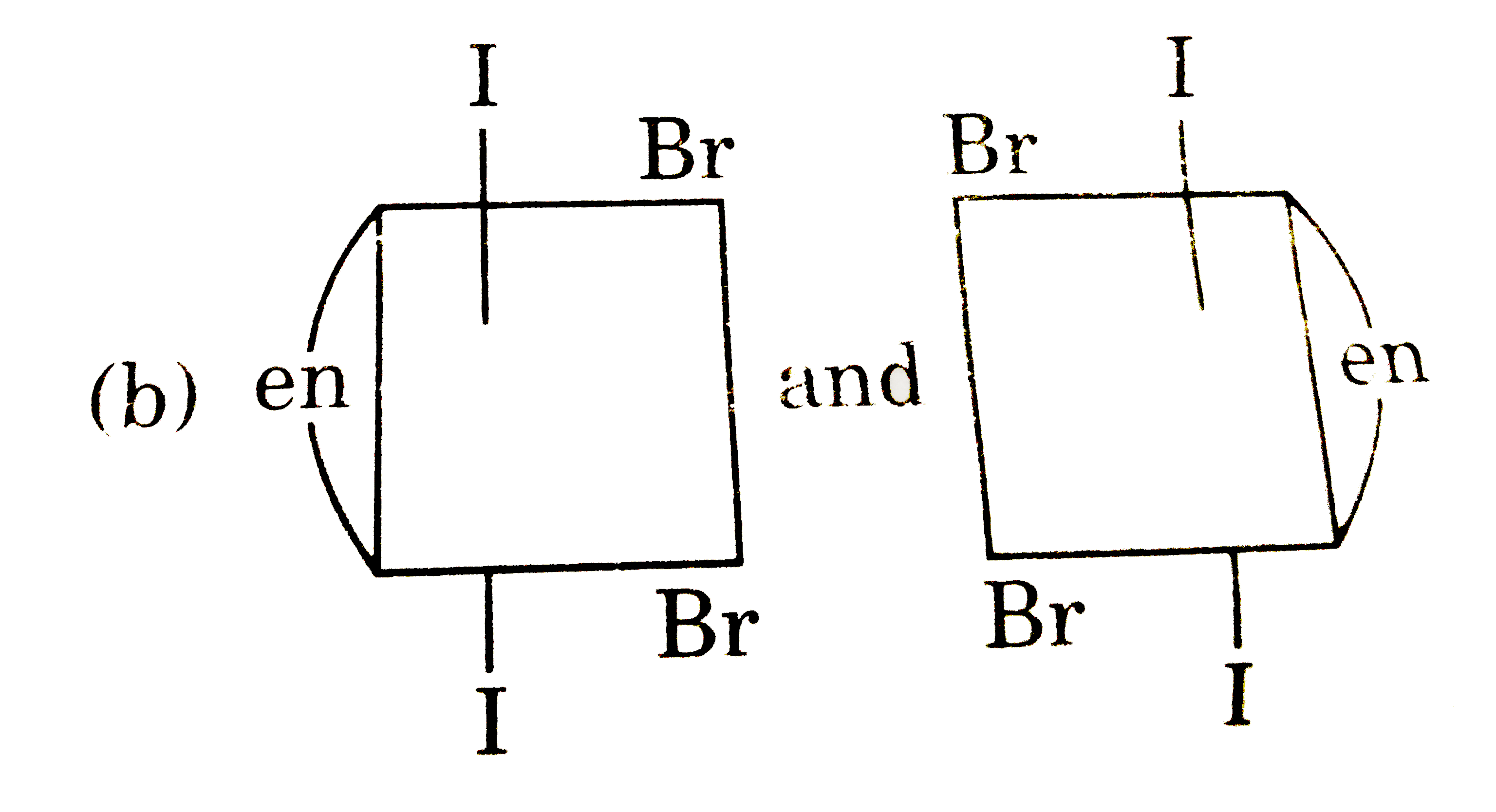
C

D
Video Solution
Text Solution
The correct Answer is:D
(d) does not have COS or POS
|
Topper's Solved these Questions
- COORDINATION COMPOUNDSBOOK - GRB PUBLICATIONCHAPTER - COORDINATION COMPOUNDSEXERCISE - G. Organometallic Compounds, Synergic Bonding
52 Videos
- COORDINATION COMPOUNDSBOOK - GRB PUBLICATIONCHAPTER - COORDINATION COMPOUNDSEXERCISE - REASONING TYPE
59 Videos
- COORDINATION COMPOUNDSBOOK - GRB PUBLICATIONCHAPTER - COORDINATION COMPOUNDSEXERCISE - E. Stability, Colour and Magnetic Properties of Complexes
60 Videos
- CHEMICAL KINETICSBOOK - GRB PUBLICATIONCHAPTER - CHEMICAL KINETICSEXERCISE - Subjective Type
63 Videos
- D-BLOCK ELEMENTSBOOK - GRB PUBLICATIONCHAPTER - D-BLOCK ELEMENTSEXERCISE - Subjective Type
18 Videos
Similar Questions
Knowledge Check
The complex ion has two optical isomers. Their correct configuration are :
A B
B C
C D
D
The complex ion [Co(en)2Cl2]+ exhibits
Acis-trans isomerism onlyBcis-trans isomerism and optical isomerismCcis-trans isomerism and linkage isomerismDoptical isomerism and linkage isomerism.The complex ion [Co(en)2Cl2]+ exhibits
Acis-trans isomerism onlyBcis-trans isomerism and linkage isomerismCcis-trans isomerism and optical isomerismDoptical isomerism and linkage isomerism.
In the complex ion, [Co(en)2Br2]+, the oxidation number of Co is
View SolutionThe complex [Pd(en)2]2+ has....Structure
View SolutionFor the given complex [CoCl2(en)(NH3)2]+, the number of geometrical isomers, the number of optical isomers and total number of isomers of all type possible respectively are
View SolutionFor the given complex [CoCl2(en)(NH3)2]+, the number of geometrical isomers, the number of optical isomers and total number of isomers of all type possible respectively are
View SolutionTwo statements 'A' and 'R' are given below Select your answers to these items using the codes given below:
Assertion(A) : The complex ion cis−[Co(en)2Cl2]+ is optically active
Reason (R) : It is an octahedral complex
View Solution
