A cylinder is filled with a liquid of refractive index μ. The radius of the cylinder is decreasing at a constant rate K. The volume of the liquid inside the container remains constant at V. The observer and the object O are in a state of rest at a distance L from each other. When radius of cylinder is r the apparent velocity of the object as seen by the observer is 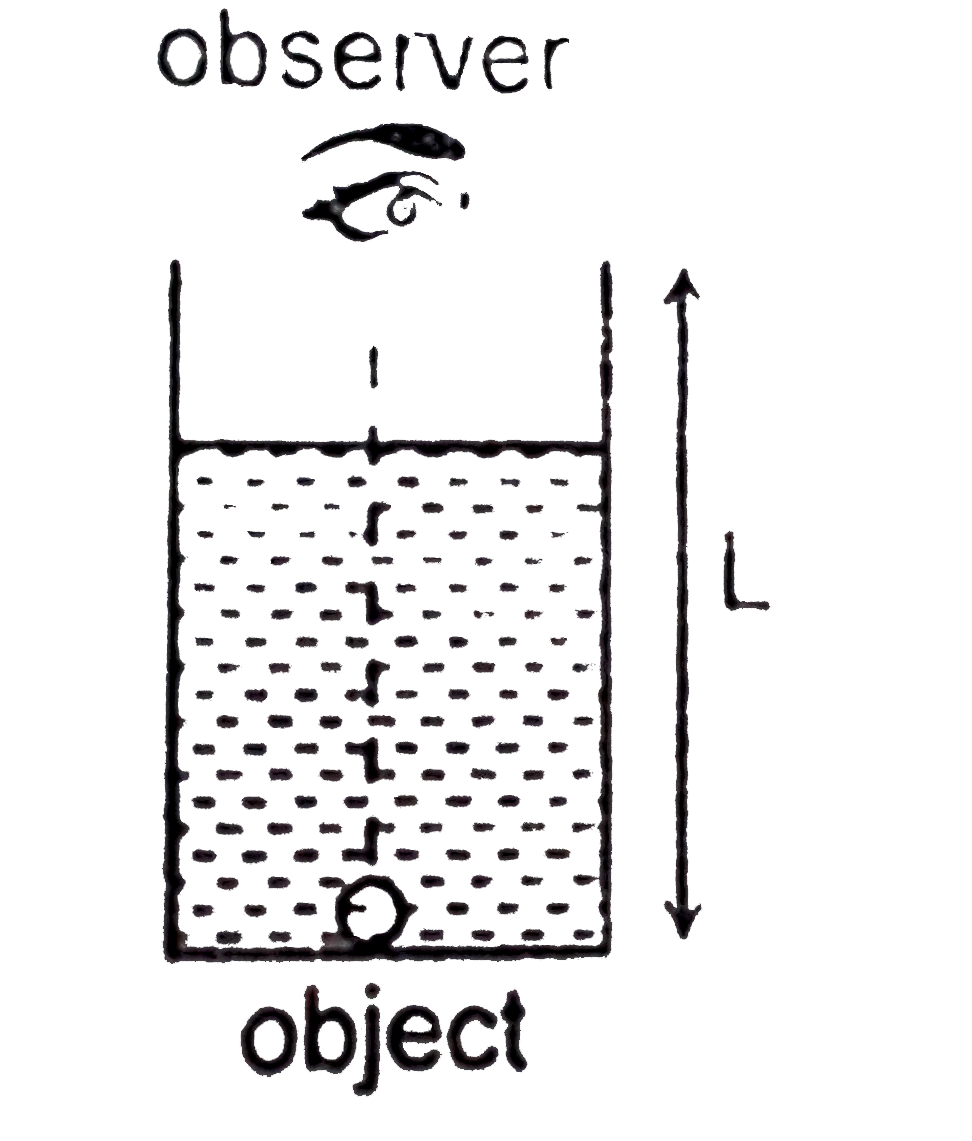
(1−μ)2KV(πμr3)
(1−μ)2KV(πμlr2)
(1−μ)2Kμ
(1−μ)K2μ
The correct Answer is:A
Xapp=L−H+Hμ 
dXappdt=dHdt(1−μμ)
πr2H=V
∴dHdt=−2Hrdrdt+2KHr
∴dXappdt=2KVπr3((1−μ)μ)
Similar Questions
Radius of a cylinder is r and the height is h. Find the change in the volume if the
height remains same and the radius is halved.
View SolutionThe apparent depth of an object at the bottom of tank filled with a liquid of refractive index 1.3 is 7.7 cm. what is the actual depth of the liquid in the tank ?
View Solution
Knowledge Check
The radius of the base of a cylinder is 14 cm and height is 6 cm. The volume of the cylinder is :
A196 πB392 πC1176πDNone of theseHeight and radius of a cylinder are increased by 10%, then the volume of the cylinder, is
A0.331B0.4C0.1D1A cylinder is inscribed in a sphere of radius r
What is the radius of the cylinder of maximum volume ?A2r√3B√2√3rCrD√3r
The radius and height of a cylinder are in the ratio 7:2. If the volume of the cylinder is 8316cm3, find the total surface ara of the cylinder.
View SolutionA cylinder is inscribed in a sphere of radius R. The volume V of the cylinder is written as v=f(x),wherex is the height of the cylinder
View SolutionThe radius of a circular cylinder is the same as that of a sphere. Their volumes are equal. The height of the cylinder is ---
View SolutionThe radius of the cylinder of maximum volume, which can be inscribed in a sphere of radius R is
View SolutionIf the volume of the cylinder is 3564 cm3. The external radius of the cylinder is 12 cm and thickness is 3 cm. Then find the length of the cylinder.
View Solution
