Two wires have identical lengths and areas of cross-section are suspended by mass M. Their Young's modulus are in the ratio 2:5.
They will be subjected to stresses which are in ratio 2:5
Their lengths will increase in the ratio 5:2
When stretched and released, they will oscillate with time periods in the ratio 5:2
Their time periods will be in the ratio √5:√2
NA
Similar Questions
Two wires of equal length and cross-sectional area are suspended as shown in figure. Their Young's modullare Y1 andY2 respectively. The equivalent Young's modulil will bebr>
View SolutionTwo wires of equal length and cross sectional area suspended as shown in
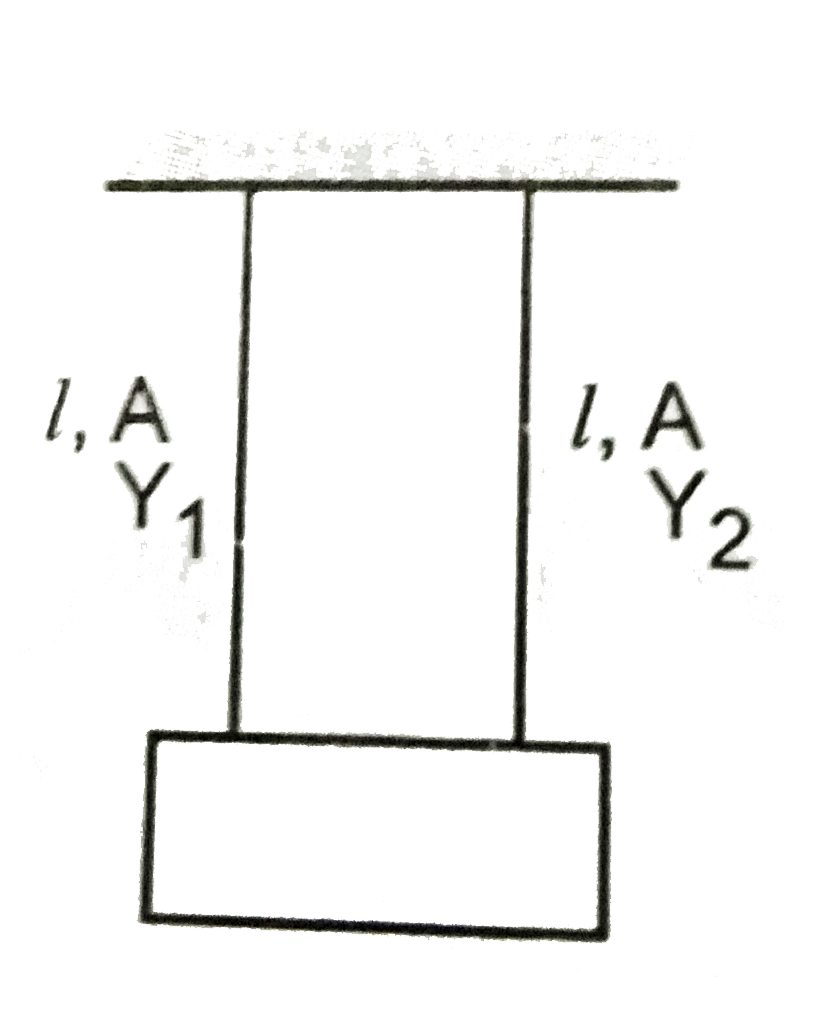
Their Young's modulii are Y1=2×1011 Pa and Y2=0.90×1011 Pa respectively. What will be the equivalent Young's modulus of combination?
View Solution
Knowledge Check
Two wires of equal length and cross-sectional area are suspended as shown in figure. Their Young's modullare Y1 andY2 respectively. The equivalent Young's modulil will bebr>
 AY1+Y2BY1+Y22CY1Y2Y1+Y2D√Y1Y2
AY1+Y2BY1+Y22CY1Y2Y1+Y2D√Y1Y2Two wires of equal length and cross-section area suspended as shown in figure. Their Young's modulus are Y1 and Y2 respectively. The equavalent Young's modulus will be
 AY1+Y2BY1−Y22CY1Y2Y1+Y2D√Y1Y2
AY1+Y2BY1−Y22CY1Y2Y1+Y2D√Y1Y2Two springs of equal lengths and equal cross sectional area are made of materials whose young's moduli are in the ratio of 3 : 2. They are suspended and loaded with the same mass. When stretched and released, they will oscillate with time period in the ratio of
A√2:√3B√3:√2C3:2D9:4
Two wires A and B have the same length and area of cross-section. But Young's modulus of A is two times the Young's modulus of B. Then the ratio of force constant of A to that of B is
View SolutionAn iron wire an copper wire having same length and cross-section are suspended form same roof Young's modulus of copper is 1/3rd that of iron. Then the ratio of the weighs to be added at their ends so that their ends are at the same level is
View SolutionTwo identical wires of materials are joined together and subjected to a force. Their Young's modulus are in the ratio 2:1 . Then their indidual extensions are in the ratio
View SolutionTwo wires A and B have the same length and area of cross-secton. But Young's modulus of A is two times the Young's modulus of B. Then the ratio of force constant of A to that of B is
View SolutionA wire of natural length l, young's modulus Y and ares of cross-section A is extended by x. Then, the energy stored in the wire is given by
View Solution
