A wire of natural length l, young's modulus Y and ares of cross-section A is extended by x. Then, the energy stored in the wire is given by
12YAlx2
13YAlx2
12YlAx2
12YAl2x2
The correct Answer is:A
To find the energy stored in a wire that has been extended, we can follow these steps:
Step 1: Understand the parameters given
We have:
- Natural length of the wire, L
- Young's modulus, Y
- Area of cross-section, A
- Extension of the wire, x
Step 2: Recall the formula for energy stored in a stretched wire
The energy stored in a wire when it is stretched is given by the formula:
Energy=12×Young's Modulus×Strain2×Volume
Step 3: Calculate the strain
Strain is defined as the change in length per unit length. Here, the change in length (extension) is x and the original length is L. Therefore, the strain ϵ can be expressed as:
Strain=ΔLL=xL
Step 4: Calculate the volume of the wire
The volume V of the wire can be calculated using the formula:
Volume=Area×Length=A×L
Step 5: Substitute the values into the energy formula
Now, substituting the values of strain and volume into the energy formula:
Energy=12×Y×(xL)2×(A×L)
Step 6: Simplify the expression
Now, simplify the expression:
Energy=12×Y×x2L2×(A×L)
=12×Y×A×x2L
Final Result
Thus, the energy stored in the wire is:
Energy=Y⋅A⋅x22L
Conclusion
The energy stored in the wire when it is extended by x is given by:
Energy=Y⋅A⋅x22L
We have:
- Natural length of the wire, L
- Young's modulus, Y
- Area of cross-section, A
- Extension of the wire, x
The energy stored in a wire when it is stretched is given by the formula:
Energy=12×Young's Modulus×Strain2×Volume
Strain is defined as the change in length per unit length. Here, the change in length (extension) is x and the original length is L. Therefore, the strain ϵ can be expressed as:
Strain=ΔLL=xL
The volume V of the wire can be calculated using the formula:
Volume=Area×Length=A×L
Now, substituting the values of strain and volume into the energy formula:
Energy=12×Y×(xL)2×(A×L)
Now, simplify the expression:
Energy=12×Y×x2L2×(A×L)
=12×Y×A×x2L
Thus, the energy stored in the wire is:
Energy=Y⋅A⋅x22L
The energy stored in the wire when it is extended by x is given by:
Energy=Y⋅A⋅x22L
Topper's Solved these Questions
Similar Questions
Two wires have identical lengths and areas of cross-section are suspended by mass M. Their Young's modulus are in the ratio 2:5.
View SolutionA wire of given metarial having length l and ares of cross-section A has a resistance of 4Ω. What would be the resistance of another wire of the same meterial having length l/2 and area of cross-section 2A ?
View Solution
Knowledge Check
A wire of length L and area of cross-section A, is stretched by a load. The elongation produced in the wire is I. If Y is the Young's modulus of the material of the wire, then the torce corstant of the wire is
AYLABYlACYALDYAlA block of mass M is suspended from a wire of length L, area of cross-section A and Young's modulus Y. The elastic potential energy stored in the wire is
A12M2g2LAYB12MgALYC12M2g2AYLD12MgYALIf a uniform brass wire of length 5 m and radius 10−3 m is extended by 10−3m, then the energy stored in the wire will be
(Young's modulus for brass =10×1010N/m2)A3.14×10−2JB3.14×10−1JC2×10−3JD3.14×10−4J
A wire extends by 'l' on the application of load 'mg'. Then the energy stored in it is
View SolutionIf Y is the Young's modulus of a wire of cross sectional area A, then the force required to increase its length by 0.1% will be
View SolutionA wire of length L, density ρ and young's modulus Y produces an elongation 1 in wire by applying load, then frequency of wire is
View SolutionWhen a force is applied at one end of an elastic wire, it produce a strain E in the wire. If Y is the Young's modulus of the material of the wire, the amount of energy stored per unit volume of the wire is given by
View SolutionA wire is length 2l, radius r and Young's modulus Y pulled perpendicular to its mid point by a distance y. Fina the tesnion in the wire
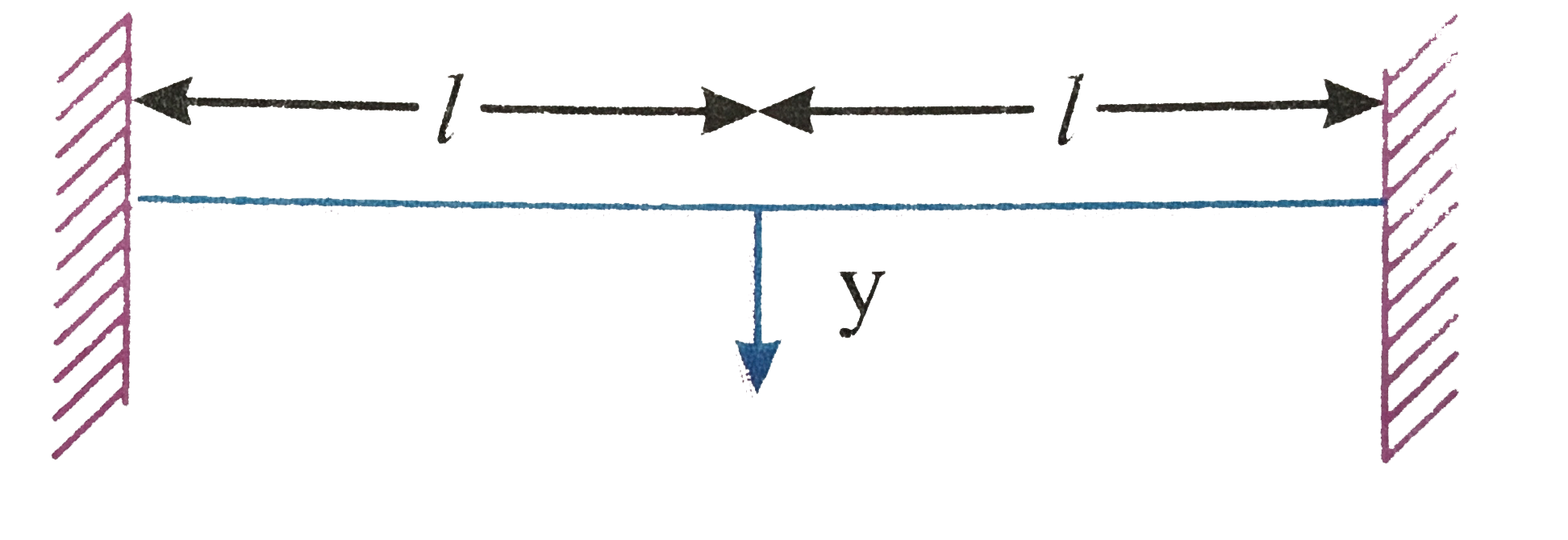
View Solution
