A rod of length l is placed along x - axis. One of its ends is at the origin. The rod has a non - uniform charge density λ=ax, a being a positive constant. The electric potential at the point P (origin) as shown in the figure is
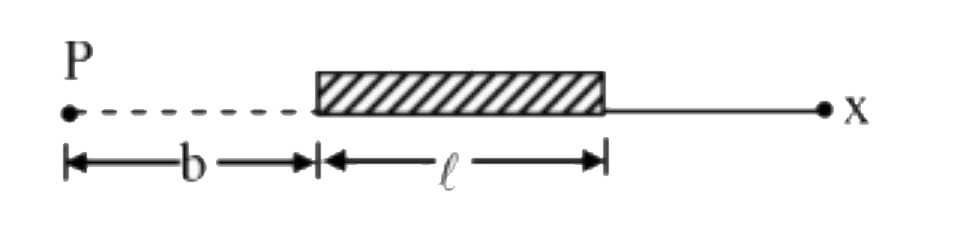
V=a4πε0(lb(b+l))
V=a4πε0(bl(b+l))
V=a4πε0(bl)
V=a4πε0(lb)
The correct Answer is:A
Step by step video, text & image solution for A rod of length l is placed along x - axis. One of its ends is at the origin. The rod has a non - uniform charge density lambda=(a)/(x), a being a positive constant. The electric potential at the point P (origin) as shown in the figure is by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
A rod of length L lies along the x-axis with its left end at the origin. It has a non-uniform charge density λ=αx, where a is a positive constant.
(a) What are the units of α?
(b) Calculate the electric potential at point A where x=−d .
View SolutionA non-uniform thin rod of length L is palced along X-axis so that one of its ends is at the origin. The linear mass density of rod is λ=λ0x. The centre of mass of rod divides the length of the rod in the ratio:
View Solution
Knowledge Check
A rod of length 'l' is placed along x-axis. One of its ends is at the origin. The rod has a non-uniform charge density λ= a, a being a positive constant. Electric potential at P as shown in the figure is -
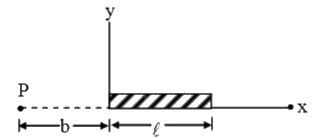 Aa4πε0ln(b+lb)Ba4πε0lnlbCa4πε0lnblDzero
Aa4πε0ln(b+lb)Ba4πε0lnlbCa4πε0lnblDzeroAn electric dipole is placed along x-axis with its centre at origin:
AThe electric field is perpendicular to each and every point on y−z planeBy−z plane is an equipotential surfaceCy−z plane is not equipotential surfaceDFlux of electrix field enclosing dipole is zeroA non–uniform thin rod of length L is placed along x-axis as such its one of ends at the origin. The linear mass density of rod is λ=λ0x. The distance of centre of mass of rod from the origin is :
AL/2B2L/3CL/4DL/5
A rod of length L is placed along the x-axis between x=0 and x=L. The linear mass density is λ such that λ=a+bx. Find the mass of the rod.
View SolutionA rod of length L is placed along the x-axis between x = 0 and x = L. The linear density (mass/ length) λ of the rod varies with the distance x from the origin as λ=Rx. Here, R is a positive constant. Find the position of centre of mass of this rod.
View SolutionA rod length L and mass M is placed along the x-axis with one end at the origin, as shown in the figure above. The rod has linear mass density λ=2ML2x, where x is the distance from the origin. Which of the following gives the x-coordinate of the rod's center of mass?

View SolutionA rod lies along the X-axis with one end at the origin and the other at x→∞. It carries a uniform charge λCm−1. The electric field at the point x=−a on the axis will be
View SolutionA rod lies along the x-axis with one end at the origin and the other at x→∞. It carries a uniform charge λ C/m. The electric field at the point x = -a on the axis will be
View Solution
