A(2a,4a),B(2a,6a),C(2a+√3a,5a) then ΔABC is .......triangle. Solution in Telugu
scalene
isosceles
equilateral
none
The correct Answer is:C
Step by step video, text & image solution for A(2a , 4a) , B(2a , 6a), C(2a + sqrt(3)a , 5a ) then DeltaABC is .......triangle. by Maths experts to help you in doubts & scoring excellent marks in Class 10 exams.
Topper's Solved these Questions
- BOOK - VGS PUBLICATION-BRILLIANTCHAPTER - COORDINATE GEOMETRY EXERCISE - Cce model examination1videos
COORDINATE GEOMETRY
- BOOK - VGS PUBLICATION-BRILLIANTCHAPTER - APPLICATIONS OF TRIGONOMETRYEXERCISE - EXERCISE154videos
APPLICATIONS OF TRIGONOMETRY
- BOOK - VGS PUBLICATION-BRILLIANTCHAPTER - COORDINATE GEOMETRY (MULTIPLE CHOICE QUESTION)EXERCISE - COORDINATE GEOMETRY(MULTIPLE CHOICE QUESTION)30videos
COORDINATE GEOMETRY (MULTIPLE CHOICE QUESTION)
Similar Questions
Find the distance between the points ( 5 , 7) and ( 7 , 5) .
03:01View SolutionDraw diagram for the following situtions :
A person is flying a kite at an angle of elevation α and the length of thread from his hand to kite is 'l'.04:46View SolutionFind the perpendicular distance of that point (3,-4) from the line 2x−5y+2=0.
08:14View SolutionProve that the points (2a,4a),(2a,6a) and (2a+sqrt(3)a,5a) are the vertices of an equilaterall triangle whose side is 2a
05:49View SolutionProve that the points (2a,4a),(2a,6a)and(2a+√3a,5a) are the vertices of an equilateral triangle.
02:59View Solutionसिद्ध कीजिये की बिंदु (2a,4a),(2a,6a) व (2a+a√3,5a) एक समबाहु त्रिभुज के शीर्ष है|
04:09View Solutionसिद्ध कीजिए कि बिंदु (2a , 4a) , (2a , 6a) तथा (2a + √3a , 5a) एक समबाहु त्रिभुज के शीर्ष हैं । समबाहु त्रिभुज के क्षेत्रफल का सूत्र लिखिए ।
03:14View Solutionसिद्ध कीजिए कि बिन्दु (2a,4a),(2a,6a) तथा (2a+√3a,5a) एक समबाहु त्रिभुज के शीर्ष हैं ।
04:04View Solution∣∣ ∣∣a+b2a+b3a+b2a+b3a+b4a+b4a+b5a+b6a+b∣∣ ∣∣=0
03:04View Solutionसिद्ध कीजिय की बिंदुएँ (2a,4a),(2a,6a) और (2a+√3a,5a) एक समबाहु त्रिभुज के शीर्ष है | जिसकी प्रत्येक भुजा की लम्बाई 2a इकाइयां है|
04:24View SolutionShow that the points (2a, 6a) (2a,4a) and (2a+√3a,5a)are the vertices of an equilateral triangle of side 2a units.
08:15View SolutionProve that (2a, 4a), (2a, 6a), and (2a +√3a, 5a) are the vertices of an equilateral triangle.
05:35View SolutionProve that the points (2a,4a),(2a,6a)and(2a+√3a,5a) are the vertices of an equilaterall triangle whose side is 2a
01:37View SolutionIf A(2a,4a),B(2a,6a) are two vartices of a ΔABC then match the vertex C given by triangle
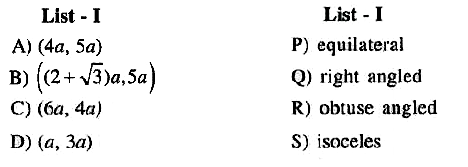 03:32View Solution
03:32View Solutionवक्तव्य । यदि A(2a,4a) तथा B(2a,6a) समबाहु ΔABC के दो शीर्ष । हैं, तब शीर्ष के निर्देशांक (2a+a√3,5a) होंगे।
वक्तव्य || एक समबाहु त्रिभुज के सभी शीर्षों के निर्देशांक परिमेय हो । सकते हैं।03:44View Solution

