The perimeter of two similar triangles are in 4:9 ratio, the ratio of their corresponding sides is…………..Solution in Telugu
9:4
2:3
16:81
4:9
The correct Answer is:D
Step by step video, text & image solution for The perimeter of two similar triangles are in 4:9 ratio, the ratio of their corresponding sides is………….. by Maths experts to help you in doubts & scoring excellent marks in Class 10 exams.
Topper's Solved these Questions
- BOOK - VGS PUBLICATION-BRILLIANTCHAPTER - SIMILAR TRIANGLES EXERCISE - CREATIVE BITS FOR CCE MODEL EXAMINATION90videos
SIMILAR TRIANGLES
- BOOK - VGS PUBLICATION-BRILLIANTCHAPTER - SIMILAR TRIANGLES EXERCISE - CREATIVE QUESTION FOR CCE MODEL EXAMINATION5videos
SIMILAR TRIANGLES
- BOOK - VGS PUBLICATION-BRILLIANTCHAPTER - SETS EXERCISE - CREATIVE BITS OF CCE MODEL EXAMINATION116videos
SETS
- BOOK - VGS PUBLICATION-BRILLIANTCHAPTER - STATISTICSEXERCISE - EXERCISE146videos
STATISTICS
Similar Questions
From the figure ,∠DAC……….
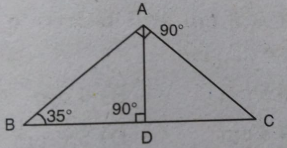 02:00View Solution
02:00View SolutionState and prove basic Proportional theorem.
02:36View SolutionLet A={1,2,{1},{1,2},3,4}, then which of the following is true?
02:58View SolutionThe mean value can be calculated from both ungrouped and grouped date . Which one you think is more accurate ? Why ?
01:17View SolutionThe ratio of corresponding sides of two similar triangles is 2:3, then the ratio of the perimeters of two triangles is 4:9 (True/False).
01:42View SolutionProve that the ratio of the perimeters of two similar triangles is the same as the ratio of their corresponding sides.
00:51View SolutionThe ratio of the areas of two similar triangles is 1:4 then the ratio of their corresponding sides………….
01:39View SolutionSides of two similar triangles are in the ratio 4 : 9 Areas of these triangles are in the ratio
03:03View SolutionThe ratio of the area of two similar triangle is 4:5, the ratio of their corresponding sides are :
03:55View SolutionThe corresponding sides of two similar triangles are in the ratio 4:9. The ratio between their areas is :
01:36View SolutionSides of two similar triangles are in the ratio 4 : 9. Areas of these triangles are in the ratio
02:43View SolutionTick the correct answer and justify : Sides of two similar triangles are in the ratio 4:9. Areas of these triangles are in the ratio
01:49View SolutionIf corresponding sides of two similar triangles are in the ratio 4 : 5 , then corresponding medians of the triangles are in the ratio 4 : k . Find K .
02:05View SolutionIf two corresponding sides of two similar triangles are in the ratio 9:4 , then what is the ratio of their areas?
03:16View SolutionIf ratio of area of two similar triangles are 16:9 then ratio of perimeter of squares formed on their corresponding sides are
01:18View Solution

