The corresponding sides of two similar triangles are in the ratio 4:9. The ratio between their areas is :Solution in Kannada
2:3
16:18
81:16
14:19
The correct Answer is:B
Step by step video, text & image solution for The corresponding sides of two similar triangles are in the ratio 4 : 9. The ratio between their areas is : by Maths experts to help you in doubts & scoring excellent marks in Class 10 exams.
Topper's Solved these Questions
- BOOK - OSWAAL PUBLICATIONCHAPTER - TRIANGLESEXERCISE - TOPIC-3 AREA OF SIMILAR TRIANGLES (VERY SHORT ANSWER TYPE QUESTIONS)6videos
TRIANGLES
- BOOK - OSWAAL PUBLICATIONCHAPTER - TRIANGLESEXERCISE - TOPIC-3 AREA OF SIMILAR TRIANGLES (SHORT ANSWER TYPE QUESTIONS)8videos
TRIANGLES
- BOOK - OSWAAL PUBLICATIONCHAPTER - TRIANGLESEXERCISE - TOPIC-1 BASIC PROPORTIONALITY THEOREM (LONG ANSWER TYPE QUESTIONS-(II))6videos
TRIANGLES
- BOOK - OSWAAL PUBLICATIONCHAPTER - SURFACE AREA AND VOLUMESEXERCISE - EXERCISE 15.55videos
SURFACE AREA AND VOLUMES
Similar Questions
What is the ratio of areas of two similar triangles whose sides are in the ratio 15:19 ?
02:42View SolutionIf the area of the similar triangles are equal, then they are congruent. Prove.
02:22View SolutionIn a ΔABC, XY∣∣BC and XY=12BC. If the area of ΔAXY=10cm2. Find the area of trapezium XYCB.
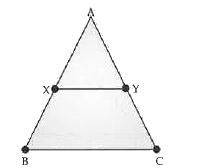 01:50View Solution
01:50View SolutionA copper wire, 3mm in diameter , is wound about a cylinder whose length is 12cm, and diameter 10cm, so as to cover the curved surface of the cylinder . Find the length and mass of the wire, assuming the density of copper to be 8.88gpercm3
02:58View SolutionIf the ratio of the sides of two similar triangles be 4:9, then ratio of areas will be
01:17View SolutionThe perimeter of two similar triangles are in 4:9 ratio, the ratio of their corresponding sides is…………..
02:26View SolutionThe ratio of the corresponding sides of two similar triangles is 5:3. Then the ratio of their areas………..
01:27View SolutionThe ratio of the areas of two similar triangles is 1:4 then the ratio of their corresponding sides………….
01:42View SolutionSides of two similar triangles are in the ratio 4 : 9 Areas of these triangles are in the ratio
01:39View SolutionArea of two similar triangles are in the ratio of 5:3 then the ratio of their corresponding sides is :
01:04View SolutionThe ratio of the areas of two similar triangles is 5:3, then ratio of their corresponding sides is :
03:03View SolutionThe ratio of the area of two similar triangle is 4:5, the ratio of their corresponding sides are :
01:36View SolutionSides of two similar triangles are in the ratio 4 : 9. Areas of these triangles are in the ratio
01:49View SolutionThe ratio between the corresponding sides of two similar triangles is 2 is to 5. Find the ratio between the areas of these triangles.
02:05View SolutionTick the correct answer and justify : Sides of two similar triangles are in the ratio 4:9. Areas of these triangles are in the ratio
03:16View Solution

