A circle with area A, is contained in the interior of a larger with area A1+A2. IF the radius of the larger circle is 3 units and A1,A2 and (A1+A2) are in A.P., then find the radius of smaller circle…..Solution in Telugu
√3units
√2units
Unity
None
The correct Answer is:A
Step by step video, text & image solution for A circle with area A, is contained in the interior of a larger with area A_1+A_2. IF the radius of the larger circle is 3 units and A_1,A_2 and (A_1+A_2) are in A.P., then find the radius of smaller circle….. by Maths experts to help you in doubts & scoring excellent marks in Class 10 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
Which of these are arithmetic progressions and why?
(i) 2,3,5,7,8,10,15, ......
View SolutionCheck whether the following equations are quadratic or not.
x2−6x−4=0
View SolutionEvaluate: △∣∣ ∣∣1+a1a2a3a11+a2a3a1a21+a3∣∣ ∣∣
View SolutionIf ratio of areas of two circle (A_1)/(A_2) is 4:1 then ratio of radius (r_1)/(r_2) is
View Solutiona_1 And a_2 And if two nonlinear single vectors abs(a_1+a_2)=sqrt3 Yes, then (a_1-a_2)*(2a_1+a_2) Will
View SolutionIf a1anda2 are two non-collinear unit vectors and if |a1+a2|=√3, then the value of (a1−a2)⋅(2a1+a2) is
View Solutionयदि A1 तथा A2 दो अरेखीय एकांक सदिश हैं तथा यदि |A1+A2|=√3, तब (A1−A2).(2A1+A2) का मान है
View Solutionयदि वृत का क्षेत्रफल A1 है तथा वृत के अंदर बने संपंचभुज का क्षेत्रफल A2 है , तब A1A2 का मान है
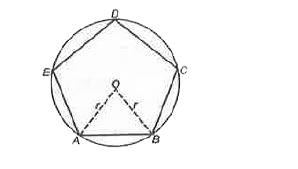
View Solutionयदि A,A1,A2,A3 किसी त्रिभुज के क्रमशः अतः वृत तथा बाह्य वृत के क्षेत्रफल हो, तो 1√A1+1√A2+1√A3 का मान है
View SolutionIf the area of the circle is A1 and the area of the regular pentagon inscribed in the circle is A2, then find the ratio A1A2.
View SolutionIf the area of the circle is A1 and the area of the regular pentagon inscribed in the circle is A2, then find the ratio A1A2.
View SolutionIf the area of the circle is A_1 and the area of the regular pentagon inscribed in the circle is A_2, then find the ratio (A_1)/(A_2)dot
View SolutionIf A,A1,A2 and A3 are the areas of the inscribed and escribed circles of a triangle, prove that 1√A=1√A1+1√A2+1√A3
View SolutionIf A,A1,A2,A3 are the areas of the inscribed and escribed circles of a ΔABC, then
View SolutionEvaluate: △∣∣ ∣∣1+a1a2a3a11+a2a3a1a21+a3∣∣ ∣∣
View Solution
