When the resistance of 9Ω is connected at the ends of a battery, its potential difference decreases from 40 volt to 30 volt . The internal resistance of the battery is
6Ω
3Ω
9Ω
15Ω
The correct Answer is:B
To find the internal resistance of the battery, we can use the following steps:
Step 1: Identify the given values
- Initial potential difference (E) = 40 V (open circuit voltage)
- Final potential difference (V) = 30 V (voltage across the load)
- Load resistance (R) = 9 Ω
Step 2: Use Ohm's Law to find the current
Ohm's law states that V=I⋅R. We can rearrange this to find the current (I) flowing through the circuit when the load is connected:
I=VR=30V9Ω=309=103A
Step 3: Apply the formula for internal resistance
The formula relating the electromotive force (E), the terminal voltage (V), the current (I), and the internal resistance (r) of the battery is given by:
E=V+I⋅r
Substituting the known values into the equation:
40V=30V+(103A)⋅r
Step 4: Solve for internal resistance (r)
Rearranging the equation to isolate r:
40V−30V=(103A)⋅r
10V=(103A)⋅r
Now, divide both sides by 103A:
r=10V103A=10V⋅310A=3Ω
Final Answer
The internal resistance of the battery is r=3Ω.
---
- Initial potential difference (E) = 40 V (open circuit voltage)
- Final potential difference (V) = 30 V (voltage across the load)
- Load resistance (R) = 9 Ω
Ohm's law states that V=I⋅R. We can rearrange this to find the current (I) flowing through the circuit when the load is connected:
I=VR=30V9Ω=309=103A
The formula relating the electromotive force (E), the terminal voltage (V), the current (I), and the internal resistance (r) of the battery is given by:
E=V+I⋅r
Substituting the known values into the equation:
40V=30V+(103A)⋅r
Rearranging the equation to isolate r:
40V−30V=(103A)⋅r
10V=(103A)⋅r
Now, divide both sides by 103A:
r=10V103A=10V⋅310A=3Ω
The internal resistance of the battery is r=3Ω.
Topper's Solved these Questions
- BOOK - ERRORLESS CHAPTER - CURRENT ELECTRICITYEXERCISE - Kirchhoff s Law, cells8videos
CURRENT ELECTRICITY
- BOOK - ERRORLESS CHAPTER - CURRENT ELECTRICITYEXERCISE - Different Measuring Instruments1videos
CURRENT ELECTRICITY
- BOOK - ERRORLESS CHAPTER - COMMUNICATION SYSTEMEXERCISE - S E T14videos
COMMUNICATION SYSTEM
- BOOK - ERRORLESS CHAPTER - ELECTRO MAGNETIC INDUCTIONEXERCISE - SET20videos
ELECTRO MAGNETIC INDUCTION
Similar Questions
the current in a circuit containing a battery connected to 2Ω resistance is 0.9A. When ana additional resistance of 8Ω is connected to the same battery the current observed in the circuit is 0.3A. Then the internal resistance of the battery is xΩ. Find value of x.
View SolutionThe emf of a battery is 6 V and its internal resistance is 0.6Ω. A wire of resistance 2.4Ω is connected to the two ends of the battery, calculate (a) current in the circuit and (b) the potential difference between the two terminals of the battery in closed circuit.
View Solution
Knowledge Check
- Question 1 - Select One
In the given figure, battery E is balanced on 55 cm length of potentiometer wire but when a resistance of 10Ω is connected in parallel with the battery then it balances on 50 cm length of the potentiometer wire then internal resistance r of the battery is
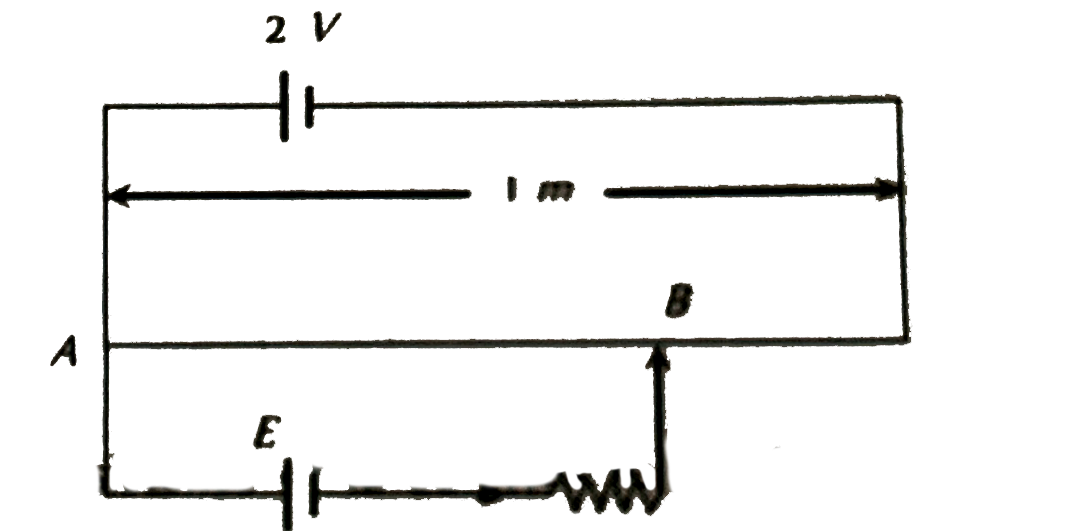 A1ΩB3ΩC10ΩD5Ω
A1ΩB3ΩC10ΩD5Ω - Question 2 - Select One
The current in a circuit containing a battery connected to 2Ω resistance is 0.9A. When a resistance of 7Ω connected to the same battery, the current observed in the circuit is 0.3 A. Then the internal resistance of te battery is
A0.1ΩB0.5ΩC1ΩDzero - Question 3 - Select One
The potential difference in open circuit for a cell is 2.2 volts. When a 4 ohm resistor is connected between its two electrodes the potential difference becomes 2 volts. The internal resistance of the cell will be
A1ohmB0.2 ohmC2.5 ohmD0.4 ohm
When a resistance of 2Ω is placed across the terminals of a battery, the current is 0.5 A. When the resistance across the terminals of the battery is 5Ω, the current is 0.25 A. Calculate the emf of the battery and also its internal resistance.
View SolutionA shortage battey with an emf of 10V and an internal resistance 1Ω is connected across an extenal resistance R and liberates of 9W power. Find the potential difference across the teminals of the battery and the value or values of R.
View SolutionA 4 m long wire of resistance 8Ω is connected in series with a battery of emf 2V and a resistor of 7Ω. The internal resistance of the battery is 1Ω. What is the potential gradient along the wire ?
View SolutionA current of 2 A flows through a 2Ω resistor when connected across a battery. The same battery supplies a current of 0.5 A when connected across a 9 Ω resistor. The internal resistance of the battery is
View SolutionA current of 2A flows through a 2Ω resistor when connected across a battery. The same battery supplies a current of 0.5A when connected across a 9Ω resistor. The internal resistance of the battery is
View Solution

