Derive1Rp=1R1+1R2+1R3.(Resistors in parallel)Solution in Telugu
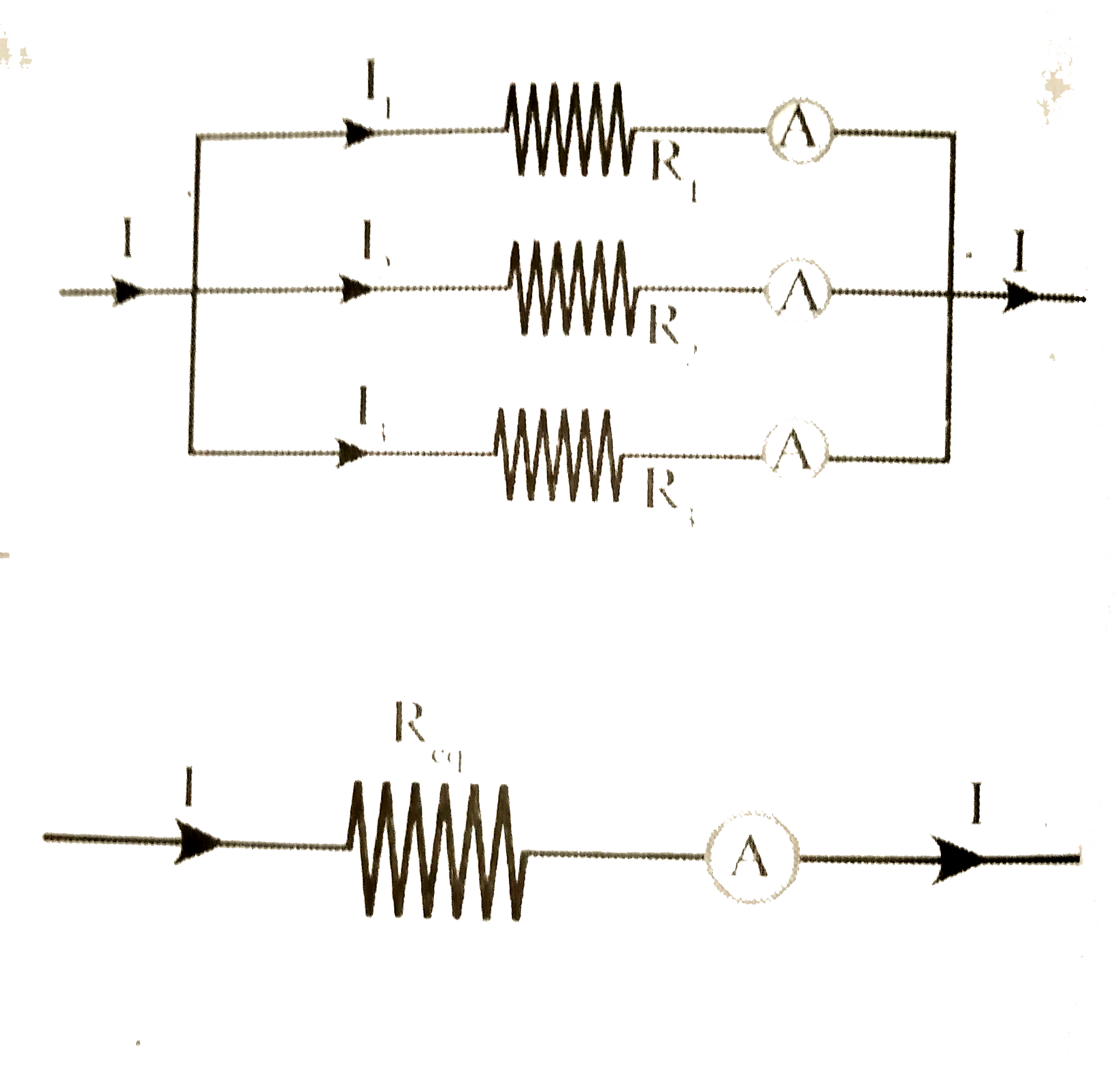
Parallel Connection : In Parallel connection of resistors there is same potential difference at the ends of the resistors. Hence the voltage in the circuit is equal to V.
Let I1,I2andI3 be the currents flowing through R1,R2andR3 resistors respectively.
Hence, we can write I=I1+I2+I3.
According to the Ohm's law.
V1=11R1,V2=I2R2,V3=I3R3
here,V=V1=V2=V3
∴V=I1R1,V=I2R2,V=I3R3
⇒I1=VR1,I2=VR2andI3=VR3
∴I=I1+I2+L3
⇒VReq=VR1+VR2+VR3
rArrcancel(V)xx(1)/(R_(eq))=cancel(V)[(1)/(R_(1))+(1)/(R_(2))+(1)/(R_(3))]
⇒1Req=1R1+1R2+1R3( here Req is the equivalent resistance )
∴ The equivalent resistance of a parallel combination is less than the resistance of each of the resistors.
Topper's Solved these Questions
- BOOK - VGS PUBLICATION-BRILLIANTCHAPTER - ELECTRIC CURRENTEXERCISE - APPLICATION TO DAILY LIFE, CONCERN TO BIODIVERSITY37videos
ELECTRIC CURRENT
- BOOK - VGS PUBLICATION-BRILLIANTCHAPTER - ELECTRIC CURRENTEXERCISE - FILL IN THE BLANKS8videos
ELECTRIC CURRENT
- BOOK - VGS PUBLICATION-BRILLIANTCHAPTER - ELECTRIC CURRENTEXERCISE - SECTION - IV (4 Marks Questions)16videos
ELECTRIC CURRENT
- BOOK - VGS PUBLICATION-BRILLIANTCHAPTER - CHEMICAL REACTIONS AND EQUATIONSEXERCISE - ESSENTIAL MATERIAL FOR EXAMINATION PURPOSE1videos
CHEMICAL REACTIONS AND EQUATIONS
- BOOK - VGS PUBLICATION-BRILLIANTCHAPTER - ELECTROMAGNETISMEXERCISE - CREATIVE QUESTION FOR NEW MODEL EXAMINATION (SEC-4)30videos
ELECTROMAGNETISM
Similar Questions
How can you appreciate the role of a small fuse in house wiring circuit in preventing damage to various electrical appliance connected in the circuit ?
03:30View SolutionThe kilowatt hour is the of ……………..
01:45View SolutionState Kirchoff Loop Law and explain.
10:10View SolutionWhy the metals displace the hydrogen from metal? Give example of activity.
06:22View SolutionHow can you verify with experiment."The magnetic field lines are closed loops"?
01:43View SolutionTwo resistors of resistance R1 and R2 having R1>R2 are connected in parallel. For equivalent resistance R, the correct statement is
View SolutionValue of 1r21+1r22+1r23+1r2 is :
06:54View SolutionProve that r1(r2+r3)√r1r2+r2r3+r3r1=a
View SolutionStatement-1: ln !ABC,r1+r2+r3−r=4R
Statement-2: In !ABC,r1r2+r2r3+r3r1=!203:02View SolutionIf r,r1,r2,r3 have their usual meanings , the value of 1r1+1r2+1r3, is
03:02View SolutionDerive R=R1+R2+R3.
View SolutionR1,R2 और R3 के तीन प्रतिरोध (i) श्रेणीक्रम में और (ii) समांतर क्रम में संयोजित किए गए है। तुल्य प्रतिरोध हेतु व्यंजक व्युत्पन्न कीजिए।
04:31View SolutionIn a ΔABC, if 2r2r3r2−r1=r3−r1 then
r1(r2+r3)√r1r2+r2r3+r3r1=02:30View SolutionFour resistors R_(1) , R_(2) , R_(3) and R_(4) are connected in parallel . The resultant resistance R is
01:27View SolutionIf resistors of resistance R_(1) and R_(2) are connected in parallel,then resultant resistance is "
02:07View Solution

